分析:(1)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可;
(2)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可;
(3)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入求出即可;
(4)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,设BP=x,根据∠B=∠D=90°和相似三角形的判定得出当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,代入后根据根的判别式进行判断即可.
解答:解:(1)存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴①
=
或②
=
,
解方程①得:x=
,
方程②得:x(10-x)=36,
x
2-10x+36=0,
△=(-10)
2-4×1×36<0,此方程无解,
∴当BP=
时,以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为
;
(2)在BD上存在2个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴①
=
或②
=
,
解方程①得:x=
,
方程②得:x(12-x)=36,
x
2-12x+36=0,
△=(-12)
2-4×1×36=0,
此方程的解为x
2=x
3=6,
∴当BP=
或6时,以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴存在2个点P,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为
或6;
(3)在BD上存在3个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
理由是:设BP=x,
∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴①
=
或②
=
,
解方程①得:x=
,
方程②得:x(15-x)=36,
x
2-15x+36=0,
△=(-15)
2-4×1×36=81,
此方程的解为x
2=3,x
3=12,
∴当BP=
或3或12时,以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴存在3个点P,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,此时BP的值为
或3或12;
(4)设BP=x,
∵AB⊥BD,CD⊥BD,
∴∠B=∠D=90°,
∴当
=
或
=
时,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似,
∴①
=
或②
=
,
解方程①得:x=
,
方程②得:x(l-x)=mn,
x
2-lx+mn=0,
△=(-l)
2-4×1×mn=l
2-4mn,
∴当l
2-4mn<0时,方程②没有实数根,
即当l
2-4mn<0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个P点;
∵当l
2-4mn=0时,方程②有1个实数根,
∴当l
2-4mn=0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的两个P点;
∵当l
2-4mn>0时,方程②有2个实数根,
∴当l
2-4mn>0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点.

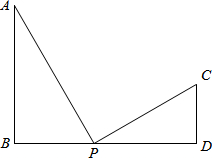 (2013•永州)如图,已知AB⊥BD,CD⊥BD
(2013•永州)如图,已知AB⊥BD,CD⊥BD

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案 (2013•永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(2013•永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3 (2013•永州)如图,两个反比例函数y=
(2013•永州)如图,两个反比例函数y= (2013•永州)如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为
(2013•永州)如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为
 (2013•永州)如图,已知二次函数y=(x-m)2-4m2(m>0)的图象与x轴交于A、B两点.
(2013•永州)如图,已知二次函数y=(x-m)2-4m2(m>0)的图象与x轴交于A、B两点.