Question

【题目】如图，Rt△ABC中，CD是斜边AB上的高，角平分线AE交CD于H，EF⊥AB于F，则下列结论中不正确的是（ ）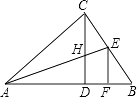

A.∠ACD=∠B
B.CH=CE=EF
C.AC=AF
D.CH=HD

Answer 1

【答案】D
【解析】解：A、∵∠B和∠ACD都是∠CAB的余角，∴∠ACD=∠B，故正确；
B、∵CD⊥AB，EF⊥AB，∴EF∥CD
∴∠AEF=∠CHE，
∴∠CEH=∠CHE
∴CH=CE=EF，故正确；
C、∵角平分线AE交CD于H，
∴∠CAE=∠BAE，
又∵∠ACB=∠AFE=90°，AE=AE，
∴△ACE≌△AEF，
∴CE=EF，∠CEA=∠AEF，AC=AF，故正确；
D、点H不是CD的中点，故错误．
故选D．
【考点精析】利用角平分线的性质定理对题目进行判断即可得到答案，需要熟知定理1：在角的平分线上的点到这个角的两边的距离相等； 定理2：一个角的两边的距离相等的点，在这个角的平分线上．