
分析 (1)根据互为顺相似和互为逆相似的定义即可作出判断;
(2)根据点P在△ABC边上的位置分为三种情况,需要分类讨论,逐一分析求解即可.
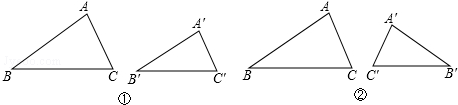
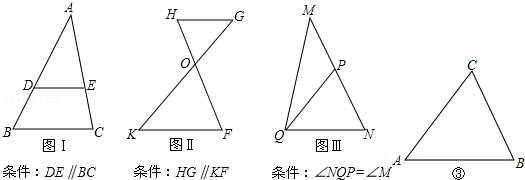
解答 解:(1)互为顺相似的是 ①②;互为逆相似的是 ③;
故答案为:①②,③;
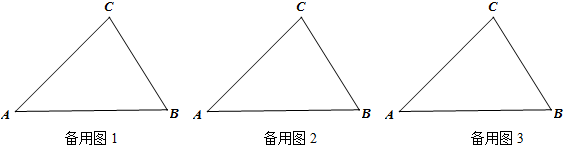
(2)根据点P在△ABC边上的位置分为以下三种情况:
第一种情况:如图①,点P在BC(不含点B、C)上,过点P只能画出2条截线PQ1、PQ2,分别使∠CPQ1=∠A,∠BPQ2=∠A,此时△PQ1C、△PBQ2都与△ABC互为逆相似.
第二种情况:如图②,点P在AC(不含点A、C)上,过点B作∠CBM=∠A,BM交AC于点M.
当点P在AM(不含点M)上时,过点P1只能画出1条截线P1Q,使∠AP1Q=∠ABC,此时△AP1Q与△ABC互为逆相似;
当点P在CM上时,过点P2只能画出2条截线P2Q1、P2Q2,分别使∠AP2Q1=∠ABC,∠CP2Q2=∠ABC,此时△AP2Q1、△Q2P2C都与△ABC互为逆相似.
第三种情况:如图③,点P在AB(不含点A、B)上,过点C作∠BCD=∠A,∠ACE=∠B,CD、CE分别交AB于点D、E.
当点P在AD(不含点D)上时,过点P只能画出1条截线P1Q,使∠AP1Q=∠ACB,此时△AQP1与△ABC互为逆相似;
当点P在DE上时,过点P2只能画出2条截线P2Q1、P2Q2,分别使∠AP2Q1=∠ACB,∠BP2Q2=∠BCA,此时△AQ1P2、△Q2BP2
都与△ABC互为逆相似;
当点P在BE(不含点E)上时,过点P3只能画出1条截线P3Q′,使∠BP3Q′=∠BCA,此时△Q′BP3与△ABC互为逆相似.
点评 本题是创新型中考压轴题,主要考查了相似三角形的知识点、分类讨论的数学思想以及接受与理解新生事物的能力.准确理解题设条件中“顺相似”“逆相似”的定义是正确解题的先决条件,在分析与解决问题的过程中,要考虑全面,进行分类讨论,避免漏解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
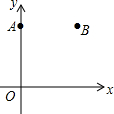 如图,在平面直角坐标系xOy中,已知点A(0,6),点B(6,6).
如图,在平面直角坐标系xOy中,已知点A(0,6),点B(6,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
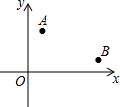 如图,在平面直角坐标系xOy中,点A(1,3),点B(5,1).
如图,在平面直角坐标系xOy中,点A(1,3),点B(5,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com