
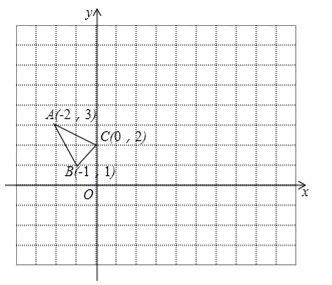
����Ŀ����ABC��ƽ��ֱ������ϵxOy�е�λ����ͼ��ʾ������д�����̣�ֱ��д�������
��1������A1B1C1���ABC����ԭ��O�����ĶԳƣ����A1������Ϊ ��
��2������ABC����ƽ��4����λ���ȵõ���A2B2C2�����B2������Ϊ ��
��3������ABC��O��˳ʱ�뷽����ת90�㣬���C�߹���·����Ϊ ��
��4����x������һ��P��ʹPA+PB��ֵ��С�����P������Ϊ ��
���𰸡���1����2����3������2����3��1������3��������4����![]() ��0����
��0����
��������
�����������1�����ù���ԭ�����ĶԳƵĵ������������⣻
��2�����õ��ƽ�ƹ�����⣻
��3����C�߹���·��Ϊ�Ե�OΪԲ�ģ�OCΪ�뾶��Բ�Ľ�Ϊ90�ȵĻ���Ȼ����ݻ�����ʽ�����C�߹���·������
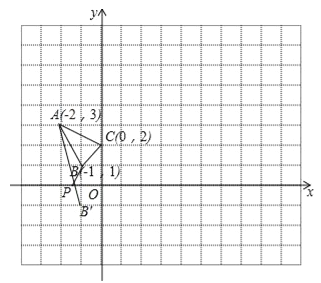
��4����ȷ����B����x��ĶԳƵ�B������Ϊ����1����1��������AB�佻x����P�㣬��������֮���߶���̿�ȷ��PA+PB��ֵ��С���������ô���ϵ�������ֱ��AB��Ľ���ʽ��Ȼ����ֱ��AB����x��Ľ�������Ϳ��õ���P�����꣮
�����������1������A1B1C1���ABC����ԭ��O�����ĶԳƣ����A1������Ϊ��2����3����
��2������ABC����ƽ��4����λ���ȵõ���A2B2C2�����B2������Ϊ��3��1����
��3������ABC��O��˳ʱ�뷽����ת90�㣬���C�߹���·����=![]() =�У�
=�У�
��4��B�����x��ĶԳƵ�B������Ϊ����1����1��������AB�佻x����P�㣬��PA+PB=PA+PB��=AB�䣬��ʱPA+PB��ֵ��С����ֱ��AB��Ľ���ʽΪy=kx+b����A����2��3����B�䣨��1����1���������![]() ������
������![]() ������ֱ��AB��Ľ���ʽΪy=��4x��5����y=0ʱ����4x��5=0�����x=
������ֱ��AB��Ľ���ʽΪy=��4x��5����y=0ʱ����4x��5=0�����x=![]() �����Դ�ʱ��P������Ϊ��
�����Դ�ʱ��P������Ϊ��![]() ��0����
��0����
�ʴ�Ϊ����2����3������3��1�����У���![]() ��0����
��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪1��=10��7�ף���25���ÿ�ѧ��������ʾΪ�� ��
A.0.25��10��5��
B.25��10��7��
C.2.5��10��6��
D.2.5��10��8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˳�������ı���ABCD���ߵ��е������ı����Ǿ��Σ����ı���ABCDһ�����㣨 ��
A.�Խ������
B.�Խ�����ƽ��
C.�Խ����ഹֱ
D.�Խ���������ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��200Ԫ,����۴�����۳���ÿ���ɻ���40Ԫ,�����Ʒ�ı��Ϊÿ��_______Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A=90�㣬EΪBC��һ�㣬A���E�����BD�Գƣ�B�㡢C�����DE�Գƣ����ABC�͡�C�Ķ�����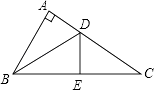
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���OΪԭ�㣬ƽ����x���ֱ����������L��![]() �ཻ��A��B���㣨��B�ڵ�һ���ޣ�����D��AB���ӳ����ϣ�
�ཻ��A��B���㣨��B�ڵ�һ���ޣ�����D��AB���ӳ����ϣ�
��1����֪a=1����B��������Ϊ2��
����ͼ1������ƽ��������Lʹ�������߹���B����AB���ӳ��߽��ڵ�C����AC�ij���
����ͼ2����BD=![]() AB������B��D��������L2���䶥��M��x���ϣ���������ߵĺ�������ʽ��
AB������B��D��������L2���䶥��M��x���ϣ���������ߵĺ�������ʽ��
��2����ͼ3����BD=AB����O��B��D�����������L3������ΪP����Ӧ�����Ķ�����ϵ��Ϊa3������P��PE��x�ᣬ��������L��E��F���㣬��![]() ��ֵ����ֱ��д��
��ֵ����ֱ��д��![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��6��6������������ABCO�Ƶ�C��ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������CDEF��ED���߶�AB�ڵ�G��ED���ӳ��߽��߶�OA�ڵ�H����CH��CG��
��1����֤����CBG�ա�CDG��
��2�����HCG�Ķ��������ж��߶�HG��OH��BG֮���������ϵ��˵�����ɣ�
��3������BD��DA��AE��EB�õ��ı���AEBD������ת�����У���G���ں�λ��ʱ�ı���AEBD�Ǿ��Σ���˵�����ɲ������H�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com