
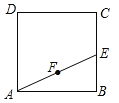
【题目】如图,正方形ABCD的面积为3cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.
【答案】![]() 或
或![]() .
.
【解析】
试题分析:如图,作DH∥MN,∵四边形ABCD是正方形,∴AD=AB,∠DAB=∠B=90°,AB∥CD,∴四边形DHMN是平行四边形,∴DH=MN=AE,在RT△ADH和RT△BAE中,∵AD=AB,DH=AE,∴△ADH≌△BAE,∴∠ADH=∠BAE,∴∠ADH+∠AHD=∠ADH+∠AMN=90°,∴∠BAE+∠AMN=90°,∴∠AFM=90°,在RT△ABE中,∵∠B=90°,AB=![]() ,∠BAE=30°,∴AEcos30°=AB,∴AE=2,在RT△AFM中,∵∠AFM=90°,AF=1,∠FAM=30°,∴AMcos30°=AF,∴AM=
,∠BAE=30°,∴AEcos30°=AB,∴AE=2,在RT△AFM中,∵∠AFM=90°,AF=1,∠FAM=30°,∴AMcos30°=AF,∴AM=![]() ,根据对称性当M′N′=AE时,BM′=
,根据对称性当M′N′=AE时,BM′=![]() ,AM′=
,AM′=![]() .故答案为:
.故答案为:![]() 或
或![]() .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
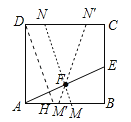
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:
当输入 ![]() 时,输出结果是299;当输入
时,输出结果是299;当输入 ![]() 时,输出结果是466;如果输入
时,输出结果是466;如果输入 ![]() 的值是正整数,输出结果是257,那么满足条件的
的值是正整数,输出结果是257,那么满足条件的 ![]() 的值最多有( )
的值最多有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表: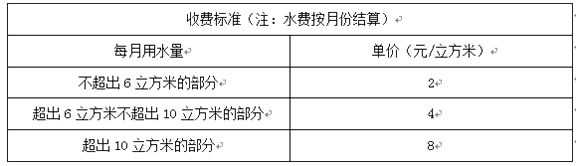
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费元;
(2)若某户居民3月份交水费36元,则用水量为立方米;
(3)若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费元.
(4)若某户居民 5、6 两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该居民5、6两个月共交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个小球从点A(3,3)出发,经过y轴上点C反弹后经过点B(1,0),则小球从A点经过点C到B点经过的最短路线长是( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。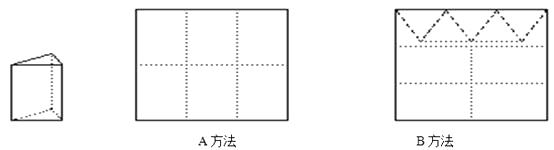
现有38张硬纸板,裁剪时x张用A方法,其余用B方法。
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.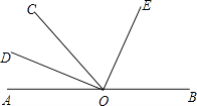
(1)请你数一数,图中有个小于平角的角;
(2)若∠AOC=50°,则∠COE的度数= , ∠BOE的度数=;
(3)猜想:OE是否平分∠BOC?请通过计算说明你猜想的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com