
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表: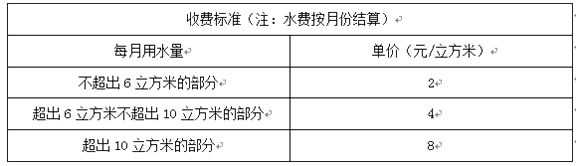
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费元;
(2)若某户居民3月份交水费36元,则用水量为立方米;
(3)若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费元.
(4)若某户居民 5、6 两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该居民5、6两个月共交水费多少元?
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
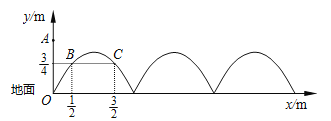
【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用![]() (a≠0)表示.已知抛物线上B,C两点到地面的距离均为
(a≠0)表示.已知抛物线上B,C两点到地面的距离均为![]() m,到墙边OA的距离分别为
m,到墙边OA的距离分别为![]() m,
m,![]() m.
m.
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组连续奇数按如图方式排列,请你解决下列问题:
(1)第7行最后一个数字是 , 在第15行第4列的数字是;
(2)请用n的代数式表示第n行的第1个数字和最后一个数字;
(3)现用一个正方形框去围出相邻两行中的4个数字
(例如:第4行和第5行的15,17,23,25),
请问能否在第50行和第51行中 围出4个数字的和是10016?若能,请求出这4个数字;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
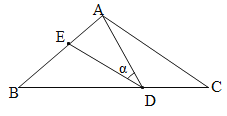
【题目】如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=![]() .有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或
.有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或![]() ;④0<BE≤
;④0<BE≤![]() ,其中正确的结论是 (填入正确结论的序号).
,其中正确的结论是 (填入正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
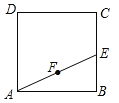
【题目】如图,正方形ABCD的面积为3cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
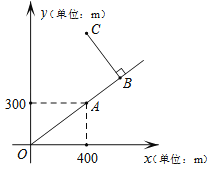
【题目】如图是根据某公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向左转90°后直行400m到达梅花阁C,则点C的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
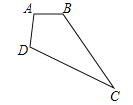
【题目】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
(2)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com