
【题目】(1)已知实数a、b在数轴上的位置如图所示,化简![]() =_____________;
=_____________;
![]()
(2)已知正整数![]() ,
,![]() 满足
满足![]() ,则整数对
,则整数对![]() 的个数是_______________;
的个数是_______________;
(3)△ABC中,∠A=50°,高BE、CF所在的直线交于点O,∠BOC的度数__________.
【答案】(1)2a-2b+1;(2)3;(3)130°或50°.
【解析】(1)∵-1<a<0,b>1,
∴![]()
=|a+1|-|a-2b|
=1+a-2b+a
=2a-2b+1.
(2)∵![]() ,
,
∴![]() ,p=2016-6
,p=2016-6![]() +9q,
+9q,
∴p=14x3(其中x为正整数),
同理可得:q=14y2(其中y为正整数),
则x+3y=12(x、y为正整数)
∴![]() ,
,
∴整数对有(p,q)=(14![]() 81,14
81,14![]() ),或(14
),或(14![]() ,或(
,或(![]() )。
)。
∴满足条件的整数对有3对.
(3)①当交点在三角形内部时(如图1),
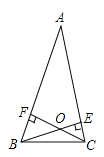
在四边形AFOE中,∠AFC=∠AEB=90°,∠A=50°,
根据四边形内角和等于360°得,
∠EOF=180°-∠A=180°-50°=130°,
故∠BOC=130°;
②当交点在三角形外部时(如图2),
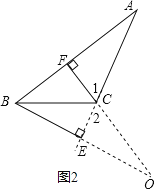
在△AFC中,∠A=50°,∠AFC=90°,
故∠1=180°-90°-50°=40°,
∵∠1=∠2,
∴在△CEO中,∠2=40°,∠CEO=90°,
∴∠EOF=180°-90°-40°=70°,
即∠BOC=50°,
综上所述:∠BOC的度数是130°或50°.
故答案是:(1). 2a-2b+1 (2). 3 (3). 130°或50°.


科目:初中数学 来源: 题型:
【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
(1)①当PC∥QB时,OQ= ;
②当PC⊥QB时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求符合下列条件的抛物线y=ax2-1的函数关系式:
(1)通过点(-3,2);
(2)与y=![]() x2的开口大小相同,方向相反;
x2的开口大小相同,方向相反;
(3)当x的值由0增加到2时,函数值减少4.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.
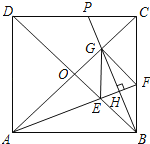
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BC∥GE,AF∥DE,∠1=50°.
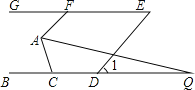
(1)求∠AFG的度数;
(2)若AQ平分∠FAC,交BC于点Q,且∠Q=15°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
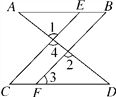
∵∠1=∠2(已知),且∠1=∠4(____________),
∴∠2=∠4(等量代换),
∴CE∥BF(__________________________),
∴∠________=∠3(______________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(__________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的方程组![]() .
.
(1)当a满足22a+3﹣22a+1=96时,求方程组的解;
(2)当程组的解满足x+y=16时,求a的值;
(3)试说明:不论a取什么实数,x的值始终为正数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=﹣3是关于x的方程(k+3)x+2=3x﹣2k的解.
(1)求k的值;
(2)在(1)的条件下,已知线段AB=6cm,点C是直线AB上一点,且BC=kAC,若点D是AC的中点,求线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com