
【题目】已知关于x、y的方程组![]() .
.
(1)当a满足22a+3﹣22a+1=96时,求方程组的解;
(2)当程组的解满足x+y=16时,求a的值;
(3)试说明:不论a取什么实数,x的值始终为正数.
【答案】(1)![]() ;(2)a=±4;(3)不论a取什么实数,
;(2)a=±4;(3)不论a取什么实数, ![]() (a+1)2+
(a+1)2+![]() 都为正数
都为正数
【解析】试题分析:先由22a+3-22a+1=96得a=2,再解方程组![]() ,即可得出方程组的解;
,即可得出方程组的解;
(2)先根据方程组![]() ,解得
,解得![]() ,再代入2x-4y=-a2+6a+6,可得2(a+9)-4(-a+7)=-a2+6a+6,进而得出a的值;
,再代入2x-4y=-a2+6a+6,可得2(a+9)-4(-a+7)=-a2+6a+6,进而得出a的值;
(3)先把![]() 消去y,可得x=
消去y,可得x=![]() a2+a+1,再进行配方,即可得出不论a取什么实数,x的值始终为正数.
a2+a+1,再进行配方,即可得出不论a取什么实数,x的值始终为正数.
试题解析:
由22a+3﹣22a+1=96得 22a+1(4﹣1)=96,
∴22a+1=32,
∴a=2,
当a=2时,方程组为
![]() ,
,
解得 ![]()
(2)由题可得方程组 ![]() ,
,
解得 ![]() ,
,
把 ![]() 代入2x﹣4y=﹣a2+6a+6,可得
代入2x﹣4y=﹣a2+6a+6,可得
2(a+9)﹣4(﹣a+7)=﹣a2+6a+6,
解得a=±4
(3)把 ![]() 消去y,可得 x=
消去y,可得 x= ![]() a2+a+1,
a2+a+1,
由配方得x= ![]() (a+1)2+
(a+1)2+ ![]() ,
,
∵不论a取什么实数, ![]() (a+1)2都为非负数,
(a+1)2都为非负数,
∴不论a取什么实数, ![]() (a+1)2+
(a+1)2+ ![]() 都为正数.
都为正数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
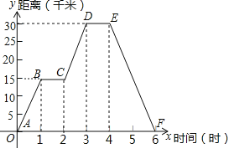
(1)根据图象回答:小明到达离家最远的地方需 小时,
(2)小明出发两个半小时离家 千米.
(3)小明出发 小时离家12千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知实数a、b在数轴上的位置如图所示,化简![]() =_____________;
=_____________;
![]()
(2)已知正整数![]() ,
,![]() 满足
满足![]() ,则整数对
,则整数对![]() 的个数是_______________;
的个数是_______________;
(3)△ABC中,∠A=50°,高BE、CF所在的直线交于点O,∠BOC的度数__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a=0.32,b=﹣3﹣2,c=![]() ,d=
,d=![]() ,则它们的大小关系是( )
,则它们的大小关系是( )
A. a<b<c<d B. b<a<d<c C. a<d<c<b D. c<a<d<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款工艺品,每件成本![]() 元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是
元,为了合理定价,现投放市场进行试销.据市场调查,销售单价是![]() 元时,每天的销售量是
元时,每天的销售量是![]() 件,若销售单价每降低
件,若销售单价每降低![]() 元,每天就可多售出
元,每天就可多售出![]() 件,但要求销售单价不得低于
件,但要求销售单价不得低于![]() 元.如果降价后销售这款工艺品每天能盈利
元.如果降价后销售这款工艺品每天能盈利![]() 元,那么此时销售单价为多少元?
元,那么此时销售单价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某钢铁企业为了适应市场竞争的需要,提高生产效率,决定将一部分钢铁生产一线员工调整去从事服务工作,该企业有钢铁生产一线员工1000人,平均每人可创造年产值30万元,根据规划,调整出去的一部分一线员工后,余下的生产一线员工平均每人全年创造年产值可增加30%,调整到服务性工作岗位人员平均每人全年可创造产值24万元,如果要保证员工岗位调整后,现在全年总产值至少增加20%,且钢铁产品的产值不能超过33150万元,怎样安排调整到服务行业的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元;
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com