
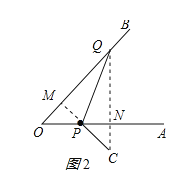
【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
(1)①当PC∥QB时,OQ= ;
②当PC⊥QB时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.

【答案】(1) 2 (2)2![]() +2 , 2
+2 , 2![]() -2 (3)符合条件的点Q共有5个. ①当点C在∠AOB内部或一边上时,OQ=2,
-2 (3)符合条件的点Q共有5个. ①当点C在∠AOB内部或一边上时,OQ=2, ![]() ,2
,2![]() ②当点C在∠AOB的外部时,OQ=
②当点C在∠AOB的外部时,OQ=![]() +
+![]() ,
, ![]() -
-![]() .
.
【解析】试题分析:(1)①由平行线的性质得出∠O=∠CPA,由折叠的性质得出∠C=∠O,OP=CP,证出∠CPA=∠C,得出OP∥QC,证出四边形OPCQ是菱形,得出OQ=OP=2cm即可;
②当PC⊥QB时,分两种情况:设OQ=xcm,证出△OPM是等腰直角三角形,得出OM= ![]() ,证出△CQM是等腰直角三角形,得出
,证出△CQM是等腰直角三角形,得出![]() ,得出方程
,得出方程![]() 解方程即可;(ii)同(i)得出:
解方程即可;(ii)同(i)得出: ![]() ,即可得出结论;
,即可得出结论;
(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;点C在∠AOB的内部或一边上时,由折叠的性质、三角形内角和定理以及解直角三角形即可求出OQ的长;点C在∠AOB的外部时,同理求出OQ的长即可;
试题解析:
(1)①当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
②当PC⊥QB时,分两种情况:
如图1所示:设OQ=xcm,

∵∠O=45°,
∴△OPM是等腰直角三角形,
∴OM=![]() ,
,
∴QM=![]() ,
,
由折叠的性质得:∠C=∠O=45°,CQ=OQ=x,
∴△CQM是等腰直角三角形,
∴QC=![]() ,
,
∴![]() ,
,
解得: ![]() ,
,
即OQ=![]() ;
;
(ii)如图2所示:
同(i)得:OQ=![]() ,
,
综上所述:当PC⊥QB时,OQ的长为![]() 或
或![]() ;
;
(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;
①点C在∠AOB的内部时,四边形OPCQ是菱形,OQ=OP=2cm;
②当点C在∠AOB的一边上时,△OPQ是等腰直角三角形,OQ=![]() 或
或![]() ,
,
③当点C在∠AOB的外部时,分两种情况:
(i)如图3所示:PM=PQ,则∠PMQ=∠PQM=∠O+∠OPQ,

由折叠的性质得:∠OPQ=∠MPQ,
设∠OPQ=∠MPQ=x,
则∠PMQ=∠PQM=45°+x,
在△OPM中,由三角形内角和定理得:45°+x+x+45°+x=180°,
解得:x=30°,
∴∠OPQ=30°,
作QN⊥OP于N,设ON=a,
∵∠O=45°,
则QN=ON=a,OQ= ![]() ,PN=
,PN=![]() ,
,
∵ON+PN=OP,
∴a+![]() ,
,
解得: ![]() ,
,
∴OQ=![]() ;
;
(ii)如图4所示:PQ=MQ,作QN⊥OA于N,

同①得:OQ=![]() ;
;
综上所述:当折叠后重叠部分为等腰三角形时,OQ的长为2cm或![]()
![]() 。
。


科目:初中数学 来源: 题型:
【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.

(1)请你利用上述方法求出△ABC的面积.
(2)在图2中画△DEF,DE、EF、DF三边的长分别为![]() 、
、![]() 、
、![]()
①判断三角形的形状,说明理由.
②求这个三角形的面积.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 是线段
是线段![]() 所在平面内任意一点,分别以
所在平面内任意一点,分别以![]() 、
、![]() 为边,在
为边,在![]() 同侧作等边
同侧作等边![]() 和等边
和等边![]() ,联结
,联结![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图1,当点![]() 在线段
在线段![]() 上移动时,线段
上移动时,线段![]() 与
与![]() 的数量关系是:________;
的数量关系是:________;
(2)如图2,当点![]() 在直线
在直线![]() 外,且
外,且![]() ,仍分别以
,仍分别以![]() 、
、![]() 为边,在
为边,在![]() 同侧作等边
同侧作等边![]() 和等边
和等边![]() ,联结
,联结![]() 、
、![]() 交于点
交于点![]() .(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时
.(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时![]() 是否随
是否随![]() 的大小发生变化?若变化,写出变化规律,若不变,请求出
的大小发生变化?若变化,写出变化规律,若不变,请求出![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,联结![]() ,求证:
,求证: ![]() 平分
平分![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边AB在数轴上,数轴上点A表示的数为﹣1,正方形ABCD的面积为16.

(1)数轴上点B表示的数为 ;
(2)将正方形ABCD沿数轴水平移动,移动后的正方形记为A′B′C′D′,移动后的正方形A′B′C′D′与原正方形ABCD重叠部分的面积为S.
①当S=4时,画出图形,并求出数轴上点A′表示的数;
②设正方形ABCD的移动速度为每秒2个单位长度,点E为线段AA′的中点,点F在线段BB′上,且BF=![]() BB′.经过t秒后,点E,F所表示的数互为相反数,直接写出t的值.
BB′.经过t秒后,点E,F所表示的数互为相反数,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
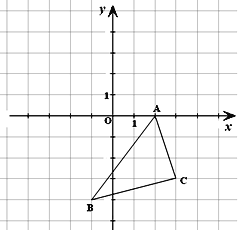
【题目】如图所示的直角坐标系中,解答下列问题:
(1)分别写出A、B两点的坐标;
(2)将△ABC向左平移3个单位长度,再向上平移5个单位长度,画出平移后的△A1B1C1;
(3)求 △A1B1C1的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,如图2所示是由图1中阴影部分拼成的一个正方形.
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2.请直接用含a,b的代数式表示S1,S2;
(2)请写出上述过程所揭示的乘法公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是__(写出全等的简写).
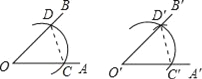
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去郊外春游,如图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
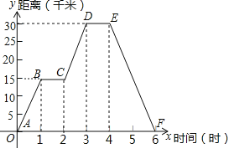
(1)根据图象回答:小明到达离家最远的地方需 小时,
(2)小明出发两个半小时离家 千米.
(3)小明出发 小时离家12千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知实数a、b在数轴上的位置如图所示,化简![]() =_____________;
=_____________;
![]()
(2)已知正整数![]() ,
,![]() 满足
满足![]() ,则整数对
,则整数对![]() 的个数是_______________;
的个数是_______________;
(3)△ABC中,∠A=50°,高BE、CF所在的直线交于点O,∠BOC的度数__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com