
【题目】已知,点![]() 是线段
是线段![]() 所在平面内任意一点,分别以
所在平面内任意一点,分别以![]() 、
、![]() 为边,在
为边,在![]() 同侧作等边
同侧作等边![]() 和等边
和等边![]() ,联结
,联结![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图1,当点![]() 在线段
在线段![]() 上移动时,线段
上移动时,线段![]() 与
与![]() 的数量关系是:________;
的数量关系是:________;
(2)如图2,当点![]() 在直线
在直线![]() 外,且
外,且![]() ,仍分别以
,仍分别以![]() 、
、![]() 为边,在
为边,在![]() 同侧作等边
同侧作等边![]() 和等边
和等边![]() ,联结
,联结![]() 、
、![]() 交于点
交于点![]() .(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时
.(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时![]() 是否随
是否随![]() 的大小发生变化?若变化,写出变化规律,若不变,请求出
的大小发生变化?若变化,写出变化规律,若不变,请求出![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,联结![]() ,求证:
,求证: ![]() 平分
平分![]() .
.

【答案】(1) ![]() ;(2)成立,证明见解析,
;(2)成立,证明见解析, ![]() ;(3) 证明见解析.
;(3) 证明见解析.
【解析】试题分析:(1)直接写出答案即可.
(2)证明ΔACD≌ΔECB,得到∠CEB=∠CAD,此为解题的关键性结论;借助内角和定理即可解决问题.
(3)过点C分别作CM⊥AD于M,CN⊥EB于N,由ΔACD≌ΔECB,得到CM=CN,从而得到结论.
试题解析:解:(1)∵△ACE、△CBD均为等边三角形,∴AC=EC,CD=CB,∠ACE=∠BCD,∴∠ACD=∠ECB;
在△ACD与△ECB中,∵AC=EC,∠ACD=∠ECB,CD=CB,∴△ACD≌△ECB(SAS),∴AD=BE,故答案为:AD=BE.
(2)AD=BE成立,∠APE不随着∠ACB的大小发生变化,始终是60°.
证明如下:
∵ΔACE和ΔBCD是等边三角形,∴AC=EC,CD=CB,∠ACE=∠BCD,∴∠BCE=∠ACD,
在ΔACD和ΔECB中,∵AC=EC,∠BCE=∠ACD,CD=CB,∴ΔACD≌ΔECB,∴AD=BE.
∵ΔACD≌ΔECB,∴∠CAD=∠CEB,∵∠APB=∠PAE+∠PEA,∴∠APB=∠CAE+∠CEA=120°,∴∠APE=60°;
(3)过点C分别作CM⊥AD于M,CN⊥EB于N,∵ΔACD≌ΔECB,∴CM=CN,∴CP平分∠DPE.



科目:初中数学 来源: 题型:
【题目】已知y=y1+y2,y1与x+1成正比例,y2与x+1成反比例,当x=0时,y=﹣5;当x=2时,y=﹣7.
(1)求y与x的函数关系式;
(2)当y=5时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用我们学过的知识,可以导出下面这个形式优美的等式:
a2+b2+c2-ab-bc-ac=![]() [(a-b)2+(b-c)2+(c-a)2],
[(a-b)2+(b-c)2+(c-a)2],
该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
(1)请你检验这个等式的正确性;
(2)若a=2 016,b=2 017,c=2 018,你能很快求出a2+b2+c2-ab-bc-ac的值吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法。
问题提出:求边长分别为![]() 的三角形面积。
的三角形面积。
问题解决:在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为![]() 的格点三角形△ABC(如图①),AB=
的格点三角形△ABC(如图①),AB=![]() 是直角边为1和2的直角三角形斜边,BC=
是直角边为1和2的直角三角形斜边,BC=![]() 是直角边分别为1和3的直角三角形的斜边,AC=
是直角边分别为1和3的直角三角形的斜边,AC=![]() 是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
是直角边分别为2和3 的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求△ABC的高,而借用网格就能计算出它的面积。
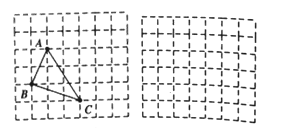
(1)请直接写出图①中△ABC的面积为_______________ 。
(2)类比迁移:求边长分别为![]() 的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
的三角形面积(请利用图②的正方形网格画出相应的△ABC,并求出它的面积)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于任意两点A(x1,y1)B (x2,y2),规定运算:
(1)A⊕B=(x1+x2,y1+y2);
(2)A⊙B=x1x2+y1y2;
(3)当x1=x2且y1=y2时,A=B.
有下列四个命题:
①若有A(1,2),B(2,﹣1),则A⊕B=(3,1),A⊙B=0;
②若有A⊕B=B⊕C,则A=C;
③若有A⊙B=B⊙C,则A=C;
④(A⊕B)⊕C=A⊕(B⊕C)对任意点A、B、C均成立.
其中正确的命题为______(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用我们学过的知识,可以导出下面这个形式优美的等式:
a2+b2+c2-ab-bc-ac=![]() [(a-b)2+(b-c)2+(c-a)2],
[(a-b)2+(b-c)2+(c-a)2],
该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.
(1)请你检验这个等式的正确性;
(2)若a=2 016,b=2 017,c=2 018,你能很快求出a2+b2+c2-ab-bc-ac的值吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
(1)①当PC∥QB时,OQ= ;
②当PC⊥QB时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求符合下列条件的抛物线y=ax2-1的函数关系式:
(1)通过点(-3,2);
(2)与y=![]() x2的开口大小相同,方向相反;
x2的开口大小相同,方向相反;
(3)当x的值由0增加到2时,函数值减少4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com