
ЁОЬтФПЁПРћгУЮвУЧбЇЙ§ЕФжЊЪЖЃЌПЩвдЕМГіЯТУцетИіаЮЪНгХУРЕФЕШЪНЃК
a2ЃЋb2ЃЋc2ЃabЃbcЃacЃН![]() [(aЃb)2ЃЋ(bЃc)2ЃЋ(cЃa)2]ЃЌ
[(aЃb)2ЃЋ(bЃc)2ЃЋ(cЃa)2]ЃЌ
ИУЕШЪНДгзѓЕНгвЕФБфаЮЃЌВЛНіБЃГжСЫНсЙЙЕФЖдГЦадЃЌЛЙЬхЯжСЫЪ§бЇЕФКЭаГЁЂМђНрУРЃЎ
(1)ЧыФуМьбщетИіЕШЪНЕФе§ШЗадЃЛ
(2)ШєaЃН2 016ЃЌbЃН2 017ЃЌcЃН2 018ЃЌФуФмКмПьЧѓГіa2ЃЋb2ЃЋc2ЃabЃbcЃacЕФжЕТ№ЃП
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉ3.
ЁОНтЮіЁПЪдЬтЗжЮіЃК(1)вбжЊЕШЪНгвБпРћгУЭъШЋЦНЗНЙЋЪНЛЏМђ,ећРэМДПЩзїГібщжЄ;
(2)Абa,b,cЕФжЕДњШывбжЊЕШЪНгвБп,ЧѓГіжЕМДЮЊЫљЧѓЪНзгЕФжЕ.
НтЃК(1)ЕШЪНгвБпЃН![]() (a2Ѓ2abЃЋb2ЃЋb2Ѓ2bcЃЋc2ЃЋa2Ѓ2acЃЋc2)
(a2Ѓ2abЃЋb2ЃЋb2Ѓ2bcЃЋc2ЃЋa2Ѓ2acЃЋc2)
ЃН![]() (2a2ЃЋ2b2ЃЋ2c2Ѓ2abЃ2bcЃ2ac)
(2a2ЃЋ2b2ЃЋ2c2Ѓ2abЃ2bcЃ2ac)
ЃНa2ЃЋb2ЃЋc2ЃabЃbcЃacЃНЕШЪНзѓБпЃЌЫљвдЕШЪНЪЧГЩСЂЕФЃЎ
(2)дЪНЃН![]() [(2 016Ѓ2 017)2ЃЋ(2 017Ѓ2 018)2ЃЋ(2 018Ѓ2 016)2]ЃН3.
[(2 016Ѓ2 017)2ЃЋ(2 017Ѓ2 018)2ЃЋ(2 018Ѓ2 016)2]ЃН3.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯBACЃН40ЁуЃЌАбЁїABCШЦзХЕуAЫГЪБеыа§зЊЃЌЪЙЕУЕуBгыCAЕФбгГЄЯпЩЯЕФЕуDжиКЯЃЌСЌНгCE.
(1)ЁїABCа§зЊСЫЖрЩйЖШЃП
(2)СЌНгCEЃЌЪдХаЖЯЁїAECЕФаЮзДЃЎ
(3)ШєЁЯACEЃН20ЁуЃЌЧѓЁЯAECЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
(1)Ѓ23ЃЋ![]() (2018ЃЋ3)0Ѓ
(2018ЃЋ3)0Ѓ![]() ЃЛЁЁЁЁЁЁ ЁЁ(2)992Ѓ69ЁС71ЃЛ
ЃЛЁЁЁЁЁЁ ЁЁ(2)992Ѓ69ЁС71ЃЛ
(3) ![]() ЁТ(Ѓ3xy)ЃЛ (4)(Ѓ2ЃЋx)(Ѓ2Ѓx)ЃЛ
ЁТ(Ѓ3xy)ЃЛ (4)(Ѓ2ЃЋx)(Ѓ2Ѓx)ЃЛ
(5)(aЃЋbЃc)(aЃbЃЋc); (6)(3xЃ2yЃЋ1)2.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЫљдкЦНУцФкШЮвтвЛЕуЃЌЗжБ№вд
ЫљдкЦНУцФкШЮвтвЛЕуЃЌЗжБ№вд![]() ЁЂ
ЁЂ![]() ЮЊБпЃЌдк
ЮЊБпЃЌдк![]() ЭЌВрзїЕШБп
ЭЌВрзїЕШБп![]() КЭЕШБп
КЭЕШБп![]() ЃЌСЊНс
ЃЌСЊНс![]() ЁЂ
ЁЂ![]() НЛгкЕу
НЛгкЕу![]() ЃЎ
ЃЎ
(1)ШчЭМ1ЃЌЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯвЦЖЏЪБЃЌЯпЖЮ
ЩЯвЦЖЏЪБЃЌЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧ:________ЃЛ
ЕФЪ§СПЙиЯЕЪЧ:________ЃЛ
(2)ШчЭМ2ЃЌЕБЕу![]() дкжБЯп
дкжБЯп![]() ЭтЃЌЧв
ЭтЃЌЧв![]() ЃЌШдЗжБ№вд
ЃЌШдЗжБ№вд![]() ЁЂ
ЁЂ![]() ЮЊБпЃЌдк
ЮЊБпЃЌдк![]() ЭЌВрзїЕШБп
ЭЌВрзїЕШБп![]() КЭЕШБп
КЭЕШБп![]() ЃЌСЊНс
ЃЌСЊНс![]() ЁЂ
ЁЂ![]() НЛгкЕу
НЛгкЕу![]() ЃЎ(1)ЕФНсТлЪЧЗёЛЙДцдкЃПШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎДЫЪБ
ЃЎ(1)ЕФНсТлЪЧЗёЛЙДцдкЃПШєГЩСЂЃЌЧыжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎДЫЪБ![]() ЪЧЗёЫц
ЪЧЗёЫц![]() ЕФДѓаЁЗЂЩњБфЛЏЃПШєБфЛЏЃЌаДГіБфЛЏЙцТЩЃЌШєВЛБфЃЌЧыЧѓГі
ЕФДѓаЁЗЂЩњБфЛЏЃПШєБфЛЏЃЌаДГіБфЛЏЙцТЩЃЌШєВЛБфЃЌЧыЧѓГі![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
(3)ШчЭМ3ЃЌдк(2)ЕФЬѕМўЯТЃЌСЊНс![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК ![]() ЦНЗж
ЦНЗж![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуDЁЂFЁЂEЁЂGЖМдкЁїABCЕФБпЩЯЃЌEFЁЮADЃЌЁЯ1=ЁЯ2ЃЌЁЯBAC=70ЁуЃЌЧѓЁЯAGDЕФЖШЪ§ЃЎЃЈЧыдкЯТУцЕФПеИёДІЬюаДРэгЩЛђЪ§бЇЪНЃЉ
НтЃКЁпEFЁЮADЃЌЃЈвбжЊЃЉ
ЁрЁЯ2=ЁЁ ЁЁЃЈЁЁ ЁЁЃЉ
ЁпЁЯ1=ЁЯ2ЃЌЃЈвбжЊЃЉ
ЁрЁЯ1=ЁЁ ЁЁЃЈЁЁ ЁЁЃЉ
ЁрЁЁ ЁЁЁЮЁЁ ЁЁЃЌЃЈЁЁ ЁЁЃЉ
ЁрЁЯAGD+ЁЁ ЁЁ=180ЁуЃЌЃЈСНжБЯпЦНааЃЌЭЌХдФкНЧЛЅВЙЃЉ
ЁпЁЁ ЁЁЃЌЃЈвбжЊЃЉ
ЁрЁЯAGD=ЁЁ ЁЁЃЈЕШЪНаджЪЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпABдкЪ§жсЩЯЃЌЪ§жсЩЯЕуAБэЪОЕФЪ§ЮЊЉ1ЃЌе§ЗНаЮABCDЕФУцЛ§ЮЊ16ЃЎ

ЃЈ1ЃЉЪ§жсЩЯЕуBБэЪОЕФЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉНЋе§ЗНаЮABCDбиЪ§жсЫЎЦНвЦЖЏЃЌвЦЖЏКѓЕФе§ЗНаЮМЧЮЊAЁфBЁфCЁфDЁфЃЌвЦЖЏКѓЕФе§ЗНаЮAЁфBЁфCЁфDЁфгыде§ЗНаЮABCDжиЕўВПЗжЕФУцЛ§ЮЊSЃЎ
ЂйЕБS=4ЪБЃЌЛГіЭМаЮЃЌВЂЧѓГіЪ§жсЩЯЕуAЁфБэЪОЕФЪ§ЃЛ
ЂкЩше§ЗНаЮABCDЕФвЦЖЏЫйЖШЮЊУПУы2ИіЕЅЮЛГЄЖШЃЌЕуEЮЊЯпЖЮAAЁфЕФжаЕуЃЌЕуFдкЯпЖЮBBЁфЩЯЃЌЧвBF=![]() BBЁфЃЎОЙ§tУыКѓЃЌЕуEЃЌFЫљБэЪОЕФЪ§ЛЅЮЊЯрЗДЪ§ЃЌжБНгаДГіtЕФжЕЃЎ
BBЁфЃЎОЙ§tУыКѓЃЌЕуEЃЌFЫљБэЪОЕФЪ§ЛЅЮЊЯрЗДЪ§ЃЌжБНгаДГіtЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
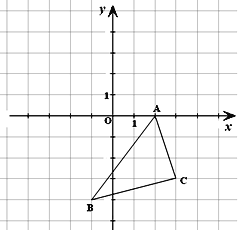
ЁОЬтФПЁПШчЭМЫљЪОЕФжБНЧзјБъЯЕжаЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЗжБ№аДГіAЁЂBСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉНЋЁїABCЯђзѓЦНвЦ3ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ5ИіЕЅЮЛГЄЖШЃЌЛГіЦНвЦКѓЕФЁїA1B1C1ЃЛ
ЃЈ3ЃЉЧѓ ЁїA1B1C1ЕФУцЛ§ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУжБГпКЭдВЙцзївЛИіНЧЕШгквбжЊНЧЕФЪОвтЭМШчЯТЃЌдђвЊЫЕУїЁЯDЁфOЁфCЁф=ЁЯDOCЃЌашвЊжЄУїЁїDЁфOЁфCЁфЁеЁїDOCЃЌдђетСНИіШ§НЧаЮШЋЕШЕФвРОнЪЧ__ЃЈаДГіШЋЕШЕФМђаДЃЉЃЎ
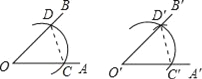
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЯьгІЙњМвНкФмМѕХХЕФКХейЃЌЙФРјОгУёНкдМгУЕчЃЌИїЪЁЯШКѓГіЬЈСЫОгУёгУЕчЁАНзЬнМлИёЁБжЦЖШЃЌШчЯТБэЪЧФГЪЁЕФЕчМлБъзМ(УПдТ)ЃЎР§ШчЃКЗНХЎЪПМв5дТЗнгУЕч500ЖШЃЌЕчЗбЃН180ЁС0.6ЃЋ220ЁСЖўЕЕЕчМлЃЋ100ЁСШ§ЕЕЕчМлЃН352дЊЃЛРюЯШЩњМв5дТЗнгУЕч460ЖШЃЌНЛЗб316дЊЃЎЧыЮЪБэжаЖўЕЕЕчМлЁЂШ§ЕЕЕчМлИїЪЧЖрЩйЃП
НзЬн | ЕчСП | ЕчМл |
вЛЕЕ | 0ЁЋ180ЖШ | 0.6дЊ/ЖШ |
ЖўЕЕ | 181ЁЋ400ЖШ | ЖўЕЕЕчМл |
Ш§ЕЕ | 401ЖШМАвдЩЯ | Ш§ЕЕЕчМл |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com