
【题目】如图,在等边三角形ABC中,BC=6cm. 射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空:当t为_________s时,四边形ACFE是菱形;
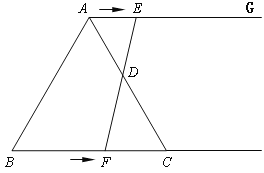
【答案】(1)证明见解析(2)①6②1.5
【解析】试题分析:(1)由题意得到AD=CD,再由AG与BC平行,利用两直线平行内错角相等得到两对角相等,利用AAS即可得证;
(2)①若四边形ACFE是菱形,则有CF=AC=AE=6,由E的速度求出E运动的时间即可;
②分两种情况考虑:若CE⊥AG,此时四点构成三角形,不是直角梯形;若AF⊥BC,求出BF的长度及时间t的值.
(1)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
∵在△ADE和△CDF中,
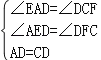 ,
,
∴△ADE≌△CDF(AAS);
(2)解:①若四边形ACFE是菱形,则有CF=AC=AE=6,
则此时的时间t=6÷1=6(s);
②四边形AFCE为直角梯形时,
(I)若CE⊥AG,则AE=3,BF=3×2=6,即点F与点C重合,不是直角梯形.
(II)若AF⊥BC,
∵△ABC为等边三角形,
∴F为BC中点,即BF=3,
∴此时的时间为3÷2=1.5(s);
故答案为:6;1.5.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】已知点(-2,y1),(-4,y,2)在函数y=x2-4x+7的图象上,那么y1,y2的大小关系是( )
A. y1>y2 B. y1= y2 C. y1<y2 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在一次扶贫助残活动中,共捐款5280000元,将5280000用科学记数法表示为( )
A. 5.28×106 B. 5.28×107
C. 52.8×106 D. 0.528×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
已知:如图,D是BC上任意一点,BE⊥AD,交AD的延长线于点E,CF⊥AD,垂足为F.
求证:∠1=∠2.
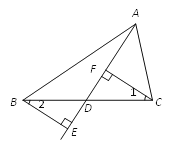
证明:∵ BE⊥AD(已知),
∴ ∠BED= °( ).
又∵ CF⊥AD(已知),
∴ ∠CFD= °.
∴ ∠BED=∠CFD(等量代换).
∴ BE∥CF( ).
∴ ∠1=∠2( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(8×106)(5×102)(2×10)=M×10a , 则M , a的值为( )
A.M=8,a=8
B.M=2,a=9
C.M=8,a=10
D.M=5,a=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P位于x轴上方,到x轴的距离为2,到y轴的距离为5,则点P坐标为( )
A. (2,5)B. (5,2)C. (2,5)或(-2,5)D. (5,2)或(-5,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
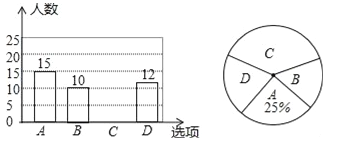
请解答下列问题:
(1)本次调查的样本容量是 ;
(2)补全条形统计图;
(3)若该学校共有3600名学生,试估计该校最想去湿地公园的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com