
【题目】完成下面的证明:
已知:如图,D是BC上任意一点,BE⊥AD,交AD的延长线于点E,CF⊥AD,垂足为F.
求证:∠1=∠2.
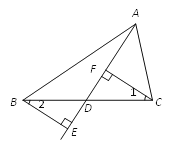
证明:∵ BE⊥AD(已知),
∴ ∠BED= °( ).
又∵ CF⊥AD(已知),
∴ ∠CFD= °.
∴ ∠BED=∠CFD(等量代换).
∴ BE∥CF( ).
∴ ∠1=∠2( ).
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
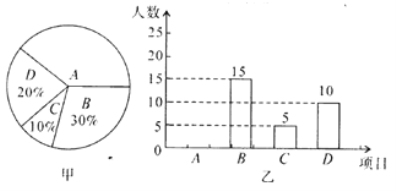
【题目】某中学开展课外体育活动,决定开设A:篮球、B:乒乓球、C:踢毽子、D:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
(1) 样本中最喜欢A项目的人数所占的百分比为 ;
(2) 请把条形统计图补充完整;
(3) 若该校有学生1700人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A.a3·(-a2)= a5
B.(-ax 2)3=-a x6
C.3x3-x(3x2-x+1)=x2-x
D.(x+1)(x-3)=x2+x-3
查看答案和解析>>
科目:初中数学 来源: 题型:
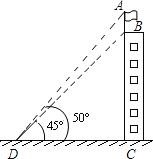
【题目】测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°,(可用的参考数据:sin50°≈0.8,tan50°≈1.2)
(1)若已知CD=20米,求建筑物BC的高度;
(2)若已知旗杆的高度AB=5米,求建筑物BC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
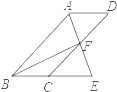
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
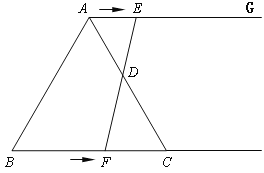
【题目】如图,在等边三角形ABC中,BC=6cm. 射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空:当t为_________s时,四边形ACFE是菱形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x+m)(x+n)=x2 -6x+5,则( )
A.m , n同时为负
B.m , n同时为正
C.m , n异 号
D.m , n异号且绝对值小 的为正
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
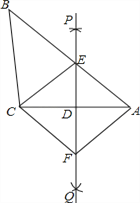
【题目】如图,在△ABC中, PQ是CA的垂直平分线, CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com