
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其顶点为点
,其顶点为点![]() ,点
,点![]() 的坐标为(0,-1),该抛物线与
的坐标为(0,-1),该抛物线与![]() 交于另一点
交于另一点![]() ,连接
,连接![]() .
.
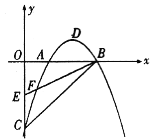
(1)求该抛物线的解析式,并用配方法把解析式化为![]() 的形式;
的形式;
(2)若点![]() 在
在![]() 上,连接
上,连接![]() ,求
,求![]() 的面积;
的面积;
(3)一动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿平行于
出发,以每秒1个单位的速度沿平行于![]() 轴方向向上运动,连接
轴方向向上运动,连接![]() ,
,![]() ,设运动时间为
,设运动时间为![]() 秒(
秒(![]() >0),在点
>0),在点![]() 的运动过程中,当
的运动过程中,当![]() 为何值时,
为何值时,![]() ?
?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)将A,B两点的坐标代入抛物线解析式中,得到关于a,b的方程组,解之求得a,b的值,即得解析式,并化为顶点式即可;
(2)过点A作AH∥y轴交BC于H,BE于G,求出直线BC,BE的解析式,继而可以求得G、H点的坐标,进一步求出GH,联立BE与抛物线方程求出点F的坐标,然后根据三角形面积公式求出△FHB的面积;
(3)设点M坐标为(2,m),由题意知△OMB是直角三角形,进而利用勾股定理建立关于m的方程,求出点M的坐标,从而求出MD,最后求出时间t.
(1)∵抛物线![]() 与
与![]() 轴交于A(1,0),B(3,0)两点,
轴交于A(1,0),B(3,0)两点,
∴![]()
∴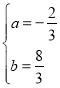
∴抛物线解析式为![]() .
.
(2)如图1,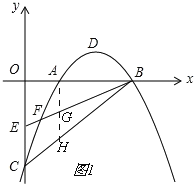
过点A作AH∥y轴交BC于H,BE于G,
由(1)有,C(0,-2),
∵B(3,0),
∴直线BC解析式为y=![]() x-2,
x-2,
∵H(1,y)在直线BC上,
∴y=-![]() ,
,
∴H(1,-![]() ),
),
∵B(3,0),E(0,-1),
∴直线BE解析式为y=-![]() x-1,
x-1,
∴G(1,-![]() ),
),
∴GH=![]() ,
,
∵直线BE:y=-![]() x-1与抛物线y=-
x-1与抛物线y=-![]() x2+
x2+![]() x-2相较于F,B,
x-2相较于F,B,
∴F(![]() ,-
,-![]() ),
),
∴S△FHB=![]() GH×|xG-xF|+
GH×|xG-xF|+![]() GH×|xB-xG|
GH×|xB-xG|
=![]() GH×|xB-xF|
GH×|xB-xF|
=![]() ×
×![]() ×(3-
×(3-![]() )
)
=![]() .
.
(3)如图2,
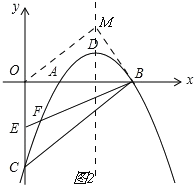
由(1)有y=-![]() x2+
x2+![]() x-2,
x-2,
∵D为抛物线的顶点,
∴D(2,![]() ),
),
∵一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,
∴设M(2,m),(m>![]() ),
),
∴OM2=m2+4,BM2=m2+1,OB2=9,
∵∠OMB=90°,
∴OM2+BM2=OB2,
∴m2+4+m2+1=9,
∴m=![]() 或m=-
或m=-![]() (舍),
(舍),
∴M(2,![]() ),
),
∴MD=![]() -
-![]() ,
,
∴t=![]() -
-![]() .
.


科目:初中数学 来源: 题型:
【题目】第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲校20名学生成绩的频数分布表和频数分布直方图如图:
甲校学生样本成绩频数分布表(表1)
成绩m(分) | 频数(人数) | 频率 |
50≤m<60 | a | 0.05 |
60≤m<70 | b | c |
70≤m<80 | 3 | 0.15 |
80≤m<90 | 8 | 0.40 |
90≤m<100 | 6 | 0.30 |
合计 | 20 | 1.0 |
b.甲校成绩在80≤m<90的这一组的具体成绩是:
87 88 88 88 89 89 89 89
c.甲、乙两校成绩的平均分、中位数、众数、方差如表所示(表2):
学校 | 平均分 | 中位数 | 众数 | 方差 |
甲 | 84 | n | 89 | 129.7 |
乙 | 84.2 | 85 | 85 | 138.6 |
根据以如图表提供的信息,解答下列问题:
(1)表1中a= ;表2中的中位数n= ;
(2)补全图1甲校学生样本成绩频数分布直方图;
(3)在此次测试中,某学生的成绩是87分,在他所属学校排在前10名,由表中数据可知该学生是 校的学生(填“甲”或“乙”),理由是 ;
(4)假设甲校200名学生都参加此次测试,若成绩80分及以上为优秀,估计成绩优秀的学生人数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )

A. (2,2![]() ) B. (﹣2,4) C. (﹣2,2
) B. (﹣2,4) C. (﹣2,2![]() ) D. (﹣2,2
) D. (﹣2,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
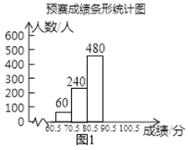
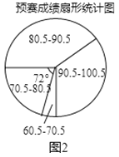
【题目】为了弘扬中华优秀传统文化,用好汉字,某中学开展了一次“古诗词”知识竞赛,赛程共分“预赛、复赛和决赛”三个阶段,预赛由各班举行,全员参加,按统一标准评分,统计成绩后绘制成如图1和图2所示的两幅不完整“预赛成绩条形统计图”和“预赛成绩扇形统计图”,预赛前10名选手参加复赛,成绩见“前10名选手成绩统计表”(采用百分制记分,得分都为60分以上的整数).
前10名选手成绩统计表
序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
预赛成绩(分) | 100 | 92 | 95 | 98 | 94 | 100 | 93 | 96 | 95 | 96 |
复赛成绩(分) | 90 | 80 | 85 | 90 | 80 | 88 | 85 | 90 | 86 | 89 |
总成绩(分) | 94 | 84.8 | 89 |
| 85.6 | 92.8 | 88.2 |
| 89.6 | 91.8 |
(1)求该中学学生的总人数,并将图1补充完整;
(2)在图2中,求“90.5~100.5分数段人数”的圆心角度数;
(3)预赛前10名选手参加复赛,成绩见“前10名选手成绩统计表”,若按预赛成绩占40%,复赛成绩占60%的比例计算总成绩,并从中选出3人参加决赛,你认为选哪几号选手去参加决赛,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线![]() 交一圆于点
交一圆于点![]() ,
,![]() ,射线
,射线![]() 交该圆于点
交该圆于点![]() ,
,![]() ,且
,且![]() .
.
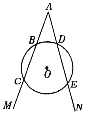
(1)判断![]() 与
与![]() 的数量关系.(不必证明)
的数量关系.(不必证明)
(2)利用尺规作图,分别作线段![]() 的垂直平分线与
的垂直平分线与![]() 的平分线,两线交于点
的平分线,两线交于点![]() (保留作图痕迹,不写作法),求证:
(保留作图痕迹,不写作法),求证:![]() 平分
平分![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进货价为30元的台灯以40元的价格售出,平均每月能售出600个,经调查表明,这种台灯的售价每上涨1元,其销量就减少10个,市场规定此台灯售价不得超过60元.
(1)为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?
(2)若商场要获得最大利润,则应上涨多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,
(1)求证:△AME∽△BEC.
(2)若△EMC∽△AME,求AB与BC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
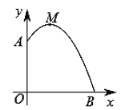
【题目】如图,某幢建筑物从2.25米高的窗口![]() 用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点
用水管向外喷水,喷的水流呈抛物线型(抛物线所在平面与墙面垂直),如果抛物线的最高点![]() 离墙1米,离地面3米,则水流下落点
离墙1米,离地面3米,则水流下落点![]() 离墙的距离
离墙的距离![]() 是( )
是( )
A.2.5米B.3米C.3.5米D.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课堂上同学们借助两个直角三角形纸板进行探究,直角三角形纸板如图所示,分别为Rt△ABC和Rt△DEF,其中∠A=∠D=90°,AC=DE=2cm. 当边AC与DE重合,且边AB和DF在同一条直线上时:

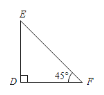
(1)在下边的图形中,画出所有符合题意的图形;

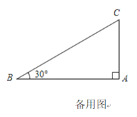
(2)求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com