
【题目】第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲校20名学生成绩的频数分布表和频数分布直方图如图:
甲校学生样本成绩频数分布表(表1)
成绩m(分) | 频数(人数) | 频率 |
50≤m<60 | a | 0.05 |
60≤m<70 | b | c |
70≤m<80 | 3 | 0.15 |
80≤m<90 | 8 | 0.40 |
90≤m<100 | 6 | 0.30 |
合计 | 20 | 1.0 |
b.甲校成绩在80≤m<90的这一组的具体成绩是:
87 88 88 88 89 89 89 89
c.甲、乙两校成绩的平均分、中位数、众数、方差如表所示(表2):
学校 | 平均分 | 中位数 | 众数 | 方差 |
甲 | 84 | n | 89 | 129.7 |
乙 | 84.2 | 85 | 85 | 138.6 |
根据以如图表提供的信息,解答下列问题:
(1)表1中a= ;表2中的中位数n= ;
(2)补全图1甲校学生样本成绩频数分布直方图;
(3)在此次测试中,某学生的成绩是87分,在他所属学校排在前10名,由表中数据可知该学生是 校的学生(填“甲”或“乙”),理由是 ;
(4)假设甲校200名学生都参加此次测试,若成绩80分及以上为优秀,估计成绩优秀的学生人数为 .

【答案】(1)1;88.5;(2)图见解析;(3)乙,乙的中位数是85,87>85;(4)140人
【解析】
(1)根据频数分布表和频数分布直方图的信息列式计算即可得到a的值,根据中位数的定义求解可得n的值;
(2)根据题意补全频数分布直方图即可;
(3)根据甲这名学生的成绩为87分,小于甲校样本数据的中位数88.5分,大于乙校样本数据的中位数85分可得;
(4)利用样本估计总体思想求解可得.
解:(1)a=20×0.05=1,
由频数分布表和频数分布直方图中的信息可知,排在中间的两个数是88和89,
∴n=![]() =88.5;
=88.5;
故答案为:1,88.5;
(2)∵b=20﹣1﹣3﹣8﹣6=2;
∴补全图1甲校学生样本成绩频数分布直方图如图所示;
(3)在此次测试中,某学生的成绩是87分,在他所属学校排在前10名,由表中数据可知该学生是乙校的学生,
理由:乙的中位数是85,87>85;
故答案为:乙,乙的中位数是85,87>85;
(4)200×![]() =140,
=140,
答:成绩优秀的学生人数为140人.
故答案为:140人.



 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】《九章算术》中有这样一个问题:“今有五雀、六燕,集称之衡,雀俱重,燕俱轻.一雀一燕交而处,衡适平.并燕、雀重一斤.问燕、雀一枚各重几何?其大意如下:今有5只雀、6只燕,分别放一起用衡器称,聚在一起的雀重,燕轻.将1只雀、1只燕交换位置放,两边重量相等.5只雀、6只燕重量为1斤(注:声代1斤=16两).问每只雀、燕各重多少两?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
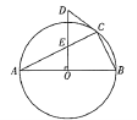
(1)若AC=4,BC=2,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax+bx-4(a,b是常数.且a![]() 0)的图象过点(3,-1).
0)的图象过点(3,-1).
(1)试判断点(2,2-2a)是否也在该函数的图象上,并说明理由.
(2)若该二次函数的图象与x轴只有一个交点,求该函数表达式.
(3)已知二次函数的图像过(![]() ,
,![]() )和(
)和(![]() ,
,![]() )两点,且当
)两点,且当![]() <
<![]()
![]()
![]() 时,始终都有
时,始终都有![]() >
>![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
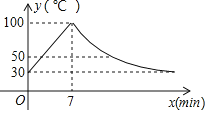
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温![]() (℃)与开机后用时
(℃)与开机后用时![]() (
(![]() )成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温
)成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温![]() (℃)与时间
(℃)与时间![]() (
(![]() )的关系如图所示:
)的关系如图所示:
(1)分别写出水温上升和下降阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)怡萱同学想喝高于50℃的水,请问她最多需要等待多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
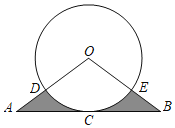
【题目】如图,AB与⊙O相切于点C,OA、OB分别交⊙O于点D、E、弧CD=弧CE
(1)求证:∠A=∠B.
(2)已知AC=2![]() ,OA=4,求阴影部分的面积.(结果保留根号和π)
,OA=4,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图所示,小吴和小黄在玩转盘游戏,准备了两个可以自由转动的转盘甲、乙,每个转盘被分成面积相等的几个扇形区域,并在每个扇形区域内标上数字,游戏规则:同时转动两个转盘,当转盘停止转动后,指针所指扇形区域内的数字之和为4,5或6时,则小吴胜;否则小黄胜.(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形区域为止)
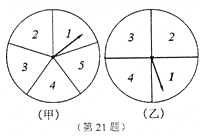
(1)这个游戏规则对双方公平吗?说说你的理由;
(2)请你设计一个对双方都公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 为
为![]() 内的一个动点,过点
内的一个动点,过点![]() 作
作![]() 与
与![]() ,使得
,使得![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
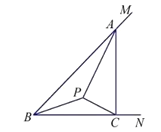
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,试求
,试求![]() 的值;
的值;
(3)记![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,且
,且![]() 、
、![]() 、
、![]() 为整数,求
为整数,求![]() 、
、![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其顶点为点
,其顶点为点![]() ,点
,点![]() 的坐标为(0,-1),该抛物线与
的坐标为(0,-1),该抛物线与![]() 交于另一点
交于另一点![]() ,连接
,连接![]() .
.
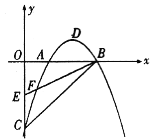
(1)求该抛物线的解析式,并用配方法把解析式化为![]() 的形式;
的形式;
(2)若点![]() 在
在![]() 上,连接
上,连接![]() ,求
,求![]() 的面积;
的面积;
(3)一动点![]() 从点
从点![]() 出发,以每秒1个单位的速度沿平行于
出发,以每秒1个单位的速度沿平行于![]() 轴方向向上运动,连接
轴方向向上运动,连接![]() ,
,![]() ,设运动时间为
,设运动时间为![]() 秒(
秒(![]() >0),在点
>0),在点![]() 的运动过程中,当
的运动过程中,当![]() 为何值时,
为何值时,![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com