
【题目】已知二次函数y=ax+bx-4(a,b是常数.且a![]() 0)的图象过点(3,-1).
0)的图象过点(3,-1).
(1)试判断点(2,2-2a)是否也在该函数的图象上,并说明理由.
(2)若该二次函数的图象与x轴只有一个交点,求该函数表达式.
(3)已知二次函数的图像过(![]() ,
,![]() )和(
)和(![]() ,
,![]() )两点,且当
)两点,且当![]() <
<![]()
![]()
![]() 时,始终都有
时,始终都有![]() >
>![]() ,求a的取值范围.
,求a的取值范围.
【答案】(1)不在;(2)![]() ;
;![]() ;(3)
;(3)![]()
【解析】
(1)将点![]() 代入函数解析式,求出a和b的等式,将函数解析式改写成只含有a的形式,再将点
代入函数解析式,求出a和b的等式,将函数解析式改写成只含有a的形式,再将点![]() 代入验证即可;
代入验证即可;
(2)令![]() ,得到一个一元二次方程,由题意此方程只有一个实数根,由根的判别式即可求出a的值,从而可得函数表达式;
,得到一个一元二次方程,由题意此方程只有一个实数根,由根的判别式即可求出a的值,从而可得函数表达式;
(3)根据函数解析式求出其对称轴,再根据函数图象的增减性判断即可.
(1)![]() 二次函数图像过点
二次函数图像过点![]()
![]() 代入得
代入得![]() ,
,![]()
![]() ,代入得
,代入得![]()
将![]() 代入得
代入得![]() ,得
,得![]() ,不成立,所以点
,不成立,所以点![]() 不在该函数图像上;
不在该函数图像上;
(2)由(1)知,![]()
![]() 与x轴只有一个交点
与x轴只有一个交点
![]() 只有一个实数根
只有一个实数根
![]() ,
,![]() 或
或![]()
当![]() 时,
时,![]() ,所以表达式为:
,所以表达式为:![]()
当![]() 时,
时,![]() ,所以表达式为:
,所以表达式为:![]() ;
;
(3)![]()
![]()
![]() 对称轴为
对称轴为![]()
当![]() 时,函数图象如下:
时,函数图象如下:

若要满足![]() 时,
时,![]() 恒大于
恒大于![]() ,则
,则![]() 、
、![]() 均在对称轴左侧
均在对称轴左侧
![]() ,
,![]()
当![]() 时,函数图象如下:
时,函数图象如下:
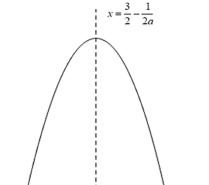
![]() ,此时
,此时![]() ,
,![]() 必小于
必小于![]()
综上,所求的a的取值范围是:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场将进货价为30元的台灯以40元的价格售出,平均每月能售出600个,经调查表明,这种台灯的售价每上涨1元,其销量就减少10个,市场规定此台灯售价不得超过60元,为了实现销售这种台灯平均每月10000元的销售利润,售价应定为多少元?这时售出台灯多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
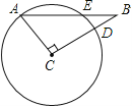
【题目】△ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有两个实数根x1,x2.
有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k使得![]() 成立?若存在,请求出k的值;若不存在,请说明理由.
成立?若存在,请求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣2mx﹣3(m≠0)与x轴交于A(3,0),B两点.
(1)求抛物线的表达式及点B的坐标;
(2)当﹣2<x<3时的函数图象记为G,求此时函数y的取值范围;
(3)在(2)的条件下,将图象G在x轴上方的部分沿x轴翻折,图象G的其余部分保持不变,得到一个新图象M.若经过点C(4.2)的直线y=kx+b(k≠0)与图象M在第三象限内有两个公共点,结合图象求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生“第二课堂“活动的选修情况,对报名参加A.跆拳道,B.声乐,C.足球,D.古典舞这四项选修活动的学生(每人必选且只能选修一项)进行抽样调查.并根据收集的数据绘制了图①和图②两幅不完整的统计图.

根据图中提供的信息,解答下列问题:
(1)本次调查的学生共有 人;在扇形统计图中,B所对应的扇形的圆心角的度数是 ;
(2)将条形统计图补充完整;
(3)在被调查选修古典舞的学生中有4名团员,其中有1名男生和3名女生,学校想从这4人中任选2人进行古典舞表演.请用列表或画树状图的方法求被选中的2人恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲校20名学生成绩的频数分布表和频数分布直方图如图:
甲校学生样本成绩频数分布表(表1)
成绩m(分) | 频数(人数) | 频率 |
50≤m<60 | a | 0.05 |
60≤m<70 | b | c |
70≤m<80 | 3 | 0.15 |
80≤m<90 | 8 | 0.40 |
90≤m<100 | 6 | 0.30 |
合计 | 20 | 1.0 |
b.甲校成绩在80≤m<90的这一组的具体成绩是:
87 88 88 88 89 89 89 89
c.甲、乙两校成绩的平均分、中位数、众数、方差如表所示(表2):
学校 | 平均分 | 中位数 | 众数 | 方差 |
甲 | 84 | n | 89 | 129.7 |
乙 | 84.2 | 85 | 85 | 138.6 |
根据以如图表提供的信息,解答下列问题:
(1)表1中a= ;表2中的中位数n= ;
(2)补全图1甲校学生样本成绩频数分布直方图;
(3)在此次测试中,某学生的成绩是87分,在他所属学校排在前10名,由表中数据可知该学生是 校的学生(填“甲”或“乙”),理由是 ;
(4)假设甲校200名学生都参加此次测试,若成绩80分及以上为优秀,估计成绩优秀的学生人数为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
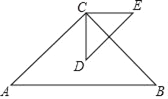
【题目】已知:如图,点D是等腰直角△ABC的重心,其中∠ACB=90°,将线段CD绕点C逆时针旋转90°得到线段CE,连结DE,若△ABC的周长为6,则△DCE的周长为( )
A. 2![]() B. 2
B. 2![]() C. 4 D. 3
C. 4 D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
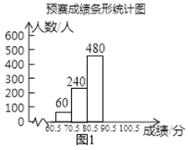
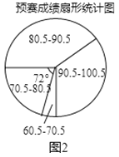
【题目】为了弘扬中华优秀传统文化,用好汉字,某中学开展了一次“古诗词”知识竞赛,赛程共分“预赛、复赛和决赛”三个阶段,预赛由各班举行,全员参加,按统一标准评分,统计成绩后绘制成如图1和图2所示的两幅不完整“预赛成绩条形统计图”和“预赛成绩扇形统计图”,预赛前10名选手参加复赛,成绩见“前10名选手成绩统计表”(采用百分制记分,得分都为60分以上的整数).
前10名选手成绩统计表
序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
预赛成绩(分) | 100 | 92 | 95 | 98 | 94 | 100 | 93 | 96 | 95 | 96 |
复赛成绩(分) | 90 | 80 | 85 | 90 | 80 | 88 | 85 | 90 | 86 | 89 |
总成绩(分) | 94 | 84.8 | 89 |
| 85.6 | 92.8 | 88.2 |
| 89.6 | 91.8 |
(1)求该中学学生的总人数,并将图1补充完整;
(2)在图2中,求“90.5~100.5分数段人数”的圆心角度数;
(3)预赛前10名选手参加复赛,成绩见“前10名选手成绩统计表”,若按预赛成绩占40%,复赛成绩占60%的比例计算总成绩,并从中选出3人参加决赛,你认为选哪几号选手去参加决赛,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com