
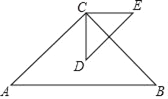
【题目】已知:如图,点D是等腰直角△ABC的重心,其中∠ACB=90°,将线段CD绕点C逆时针旋转90°得到线段CE,连结DE,若△ABC的周长为6,则△DCE的周长为( )
A. 2![]() B. 2
B. 2![]() C. 4 D. 3
C. 4 D. 3![]()
【答案】A
【解析】
延长CD交AB于F.如图,利用等腰直角三角形的性质和重心的性质得到CF平分AB,CD=2DF,则CF=![]() AB=
AB=![]() CA,所以CD=
CA,所以CD=![]() CA,再利用旋转的性质可判断△CDE为等腰直角三角形,于是可判定△CDE∽△CAB,然后根据相似三角形的性质计算△CDE的周长.
CA,再利用旋转的性质可判断△CDE为等腰直角三角形,于是可判定△CDE∽△CAB,然后根据相似三角形的性质计算△CDE的周长.
解:延长CD交AB于F.如图,
∵点D是等腰直角△ABC的重心,
∴CF平分AB,CD=2DF,
∴CF=![]() AB=
AB=![]()
![]() CA=
CA=![]() CA,
CA,
∴CD=![]() CF=
CF=![]() CA,
CA,
∵线段CD绕点C逆时针旋转90°得到线段CE,
∴CD=CE,∠DCE=90°,
∴△CDE为等腰直角三角形,
∴△CDE∽△CAB,
∴△CDE的周长:△CAB的周长=CD:CA=![]() ,
,
∴△CDE的周长=![]() ×6=2
×6=2![]() .
.
故选:A.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】综合与实践:
观察发现:①![]() ;
;
②![]() ;
;
③![]() ;
;
…
解决问题:
(1)利用你观察到的规律,化简![]() ;
;
(2)计算:![]() .
.
拓广探索:
定义:如果两个含有二次根式的非零代数式相乘,它们的积不含有二次根式,就说这两个非零代数式互为有理化因式.例如,上面计算中![]() 和
和![]() 、
、![]() 和
和![]() 等都是互为有理化因式.通过上面的观察,我们还可以发现:如果二次根式的分母原来为无理数,那么把分子、分母同乘以分母的互为有理化因式,可以将该二次根式的分母化为有理数.
等都是互为有理化因式.通过上面的观察,我们还可以发现:如果二次根式的分母原来为无理数,那么把分子、分母同乘以分母的互为有理化因式,可以将该二次根式的分母化为有理数.
(3)根据阅读,将![]() 的分母化为有理数.
的分母化为有理数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]()
(1)求证:无论![]() 取何实数值,方程总有实数根;
取何实数值,方程总有实数根;
(2)若等腰三角形![]() 的一边长
的一边长![]() ,另两边长
,另两边长![]() 、
、![]() 恰好是这个方程的两个根,求此三角形的周长
恰好是这个方程的两个根,求此三角形的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,与y轴交于C点,M点在抛物线的对称轴上,当点M到点B的距离与到点C的距离之和最小时,点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爸爸想送小明一个书包和一辆自行车作为新年礼物,在甲、乙两商场都发现同款的自行车单价相同,书包单价也相同,自行车和书包单价之和为452元,且自行车的单价比书包的单价4倍少8元.
(1)求自行车和书包单价各为多少元;
(2)新年来临赶上商家促销,乙商场所有商品打八五折(即8.5折)销售,甲全场购物毎满100元返购物券30元(即不足100元不返券,满100元送30元购物券,满200元送60元购物券),并可当场用于购物,购物券全场通用.但爸爸只带了400元钱,如果他只在同一家商场购买看中的两样物品,在哪一家买更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
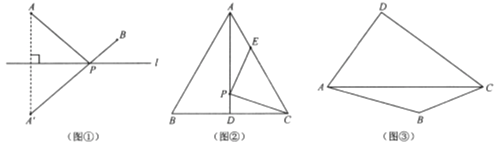
如图①,若点![]() 、
、![]() 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点![]() ,使
,使![]() 的值最小.
的值最小.
作法:作点![]() 关于直线l的对称点
关于直线l的对称点![]() ,连接
,连接![]() 交直线l于点
交直线l于点![]() ,则点
,则点![]() 即为所求.
即为所求.
【解决问题】
如图②,![]() 是边长为6cm的等边三角形
是边长为6cm的等边三角形![]() 的中线,点
的中线,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,则
上,则![]() 的最小值为 cm;
的最小值为 cm;
【拓展研究】
如图③,在四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情境![]() :小芳离开家去学校上学,走了一段路后,发现自己作业本忘家里了,于是返回家里找到作业本,然后又赶快去学校;
:小芳离开家去学校上学,走了一段路后,发现自己作业本忘家里了,于是返回家里找到作业本,然后又赶快去学校;
情境![]() :小明从家出发去图书馆还书,走了一段路程后,发现时间有点紧张,便以更快的速度前进.
:小明从家出发去图书馆还书,走了一段路程后,发现时间有点紧张,便以更快的速度前进.

(1)情境![]() 所对应的函数图象分别是_______,_______(填写序号);
所对应的函数图象分别是_______,_______(填写序号);
(2)请你为剩下的函数图象写出一个适合的情景.
查看答案和解析>>
科目:初中数学 来源: 题型:
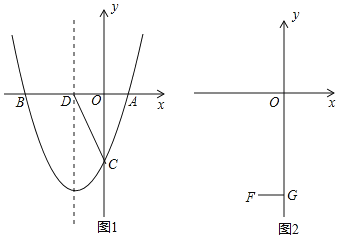
【题目】抛物线y=x2+bx+c与x轴交于A(1,0),B(m,0),与y轴交于C.
(1)若m=-3,求抛物线的解析式,并写出抛物线的对称轴;
(2)如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在抛物线对称轴左侧上有 一点E,使S△ACE=S△ACD,求E点的坐标;
(3) 如图2,设F(-1,-4),FG⊥y轴于G,在线段OG上是否存在点P,使 ∠OBP=∠FPG? 若存在,求m的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com