
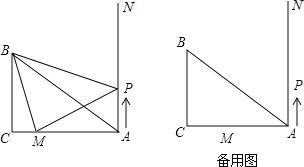
【题目】如图,在 Rt△ABC 中,∠C=90°,AC=8cm,BC=6cm,M 在 AC上,且AM=6cm,过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC,若动点 P 从点 A 出发,沿射线 AN 匀速运动,运动速度为 1cm/s,设点 P 运动时间为 t 秒.
(1)经过 秒时,Rt△AMP 是等腰直角三角形?
(2)经过几秒时,PM⊥MB?
(3)经过几秒时,PM⊥AB?
(4)当△BMP 是等腰三角形时,直接写出 t 的所有值.
【答案】(1)6;(2)2;(3)8;(4)2或![]() .
.
【解析】
(1)得出腰时AM=AP,即可得出答案;
(2)根据垂直的定义和同角的余角相等得到∠CBM=∠AMP,证明△CBM≌△AMP,根据全等三角形的性质得到 AP=CM=2,根据题意得到答案;
(3)证明△APM≌△CAB,根据全等三角形的性质得到 AP=CA=8,根据题意得到答案;
(4)分 MB=MP 和 PB=PM 两种情况,根据全等三角形的性质,勾股定理计算即可.
(1)当 Rt△AMP 是等腰直角三角形时,AP=AM=6cm,
∴t=6÷1=6(s),
故答案为:6;
(2)当 PM⊥MB 时,∠BMP=90°,
∴∠BMC+∠AMP=90°,又∠BMC+∠CBM=90°,
∴∠CBM=∠AMP,
在△CBM 和△AMP 中,
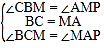 ,
,
∴△CBM≌△AMP(ASA),
∴AP=CM=2,
∴t=2,即经过 2 秒时,PM⊥MB;
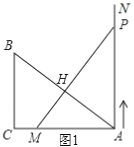
(3)当 PM⊥AB 时,如图1,∠PHA=90°,
∴∠HPA+∠HAP=90°,又∠HAP+∠CAB=90°,
∴∠APM=∠CAB,
在△APM 和△CAB 中,
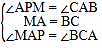 ,
,
∴△APM≌△CAB(ASA),
∴AP=CA=8,
∴t=8,
∴经过 8 秒时,PM⊥AB;
(4)根据勾股定理得,BM=![]() ,BP 的最小值为 8,
,BP 的最小值为 8,
∵![]() <8,
<8,
∴BM≠BP,
当 MB=MP 时,
在 Rt△BCM 和 Rt△MAP 中,
![]() ,
,
∴Rt△BCM≌Rt△MAP(HL),
∴AP=CM=2, 则 t=2,
当 PB=PM 时,如图2,作BF⊥AN于 F, 则四边形 BCAF 为矩形,
∴BF=CA=8,AF=BC=6,
∴PF=6﹣t,
由勾股定理得,BP2=PF2+BF2,MP2=AM2+AP2,
∴PF2+BF2=AM2+AP2,即(6﹣t)2+82=62+t2, 解得,t=![]() ,
,
∴当△BMP 是等腰三角形时,t=2 或![]() .
.


科目:初中数学 来源: 题型:
【题目】 我们定义:如图1、图2、图3,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB'C′是△ABC的“旋补三角形”,△AB′C′边B'C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.图1、图2、图3中的△AB′C′均是△ABC的“旋补三角形”.
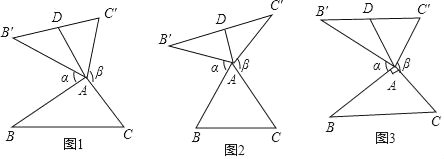
(1)①如图2,当△ABC为等边三角形时,“旋补中线”AD与BC的数量关系为:AD= BC;
②如图3,当∠BAC=90°,BC=8时,则“旋补中线”AD长为 .
(2)在图1中,当△ABC为任意三角形时,猜想“旋补中线”AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB'C′;
(2)画出△AB′C′向左平移4格后的△A′B″C″;
(3)计算线段AB在变换到AB′的过程中扫过区域的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
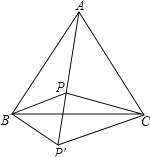
【题目】P为等边△ABC内的一点,PA=10,PB=6,PC=8,将△ABP绕点B顺时针旋转60°到△CBP′位置.
(1)判断△BPP′的形状,并说明理由;
(2)求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班抽取6名同学参加体能测试,成绩如下:85,95,85,80,80,85.下列表述错误是( )
A.众数是85
B.平均数是85
C.方差是20
D.极差是15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
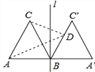
A. 4 B. 3![]() C. 2
C. 2![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠BOC=60°,OF平分∠BOC.若AO⊥BO,OE平分∠AOC,则∠EOF的度数是( )
A. 45°
B. 15°
C. 30°或60°
D. 45°或15°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com