
【题目】如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC.给出下列结论:①∠BAD=∠C;②AE=AF;③∠EBC=∠C;④FG∥AC;⑤EF=FG.其中正确的结论是_____.

【答案】①②④
【解析】
①连接EG.根据等角的余角相等即可得到结果,故①正确;②由BE、AG分别是∠ABC、∠DAC的平分线.得到∠ABF=∠EBD.由于∠AFE=∠FAB+∠FBA,∠AEG=∠C+∠EBD,得到∠AFE=∠AEF,根据等腰三角形的性质可得②正确;③如果∠EBC=∠C,则∠C=![]() ∠ABC,由于∠BAC=90°那么∠C=30°,但∠C≠30°,故③错误;④证明△ABN≌△GBN,得到AN=GN,证出四边形AFGE是平行四边形,得到GF∥AE,故④正确;⑤由AE=AF,AE=FG,而△AEF不是等边三角形,得到EF≠AE,于是EF≠FG,故⑤错误.
∠ABC,由于∠BAC=90°那么∠C=30°,但∠C≠30°,故③错误;④证明△ABN≌△GBN,得到AN=GN,证出四边形AFGE是平行四边形,得到GF∥AE,故④正确;⑤由AE=AF,AE=FG,而△AEF不是等边三角形,得到EF≠AE,于是EF≠FG,故⑤错误.
①连接EG.
∵∠BAC=90°,AD⊥BC.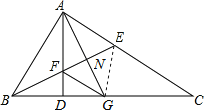
∴∠C+∠ABC=90°,∠C+∠DAC=90°,∠ABC+∠BAD=90°.
∴∠ABC=∠DAC,∠BAD=∠C,故①正确;
②∵BE、AG分别是∠ABC、∠DAC的平分线,
∴∠ABF=∠EBD.
∵∠AFE=∠FAB+∠FBA,∠AEG=∠C+∠EBD,
∴∠AFE=∠AEF.
∴AF=AE,故②正确;
③如果∠EBC=∠C,则∠C=![]() ∠ABC,
∠ABC,
∵∠BAC=90°,
那么∠C=30°,但∠C≠30°,故③错误;
④∵AG是∠DAC的平分线,
∴AN⊥BE,FN=EN,
在△ABN与△GBN中,∵![]()
∴△ABN≌△GBN.
∴AN=GN.
∴四边形AFGE是平行四边形.
∴GF∥AE.
即GF∥AC.故④正确;
⑤∵AE=AF,AE=FG,
而△AEF不是等边三角形,
∴EF≠AE.
∴EF≠FG,故⑤错误.
故答案为:①②④.


科目:初中数学 来源: 题型:
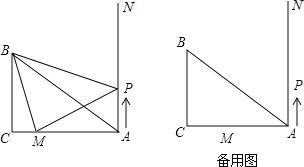
【题目】如图,在 Rt△ABC 中,∠C=90°,AC=8cm,BC=6cm,M 在 AC上,且AM=6cm,过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC,若动点 P 从点 A 出发,沿射线 AN 匀速运动,运动速度为 1cm/s,设点 P 运动时间为 t 秒.
(1)经过 秒时,Rt△AMP 是等腰直角三角形?
(2)经过几秒时,PM⊥MB?
(3)经过几秒时,PM⊥AB?
(4)当△BMP 是等腰三角形时,直接写出 t 的所有值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.2元,每天可多售出40斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,AC=20,点D与点A关于y轴对称,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.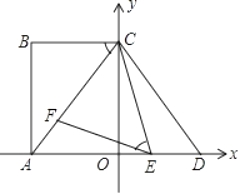
(1)直接写出BC的长是 , 点D的坐标是;
(2)证明:△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将1、![]() 、
、![]() 、
、![]() 按如图方式排列.若规定(m,n)表示第m排从左向右第n个数,则(7,3)所表示的数是__;(5,2)与(20,17)表示的两数之积是__.
按如图方式排列.若规定(m,n)表示第m排从左向右第n个数,则(7,3)所表示的数是__;(5,2)与(20,17)表示的两数之积是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察推理:如图 1,△ABC 中,∠ACB=90°,AC=BC,直线 L 过点C,点 A,B 在直线 L 同侧,BD⊥L, AE⊥L,垂足分别为D,E
求证:△AEC≌△CDB
(2)类比探究:如图 2,Rt△ABC 中,∠ACB=90°,AC=4,将斜边 AB 绕点 A 逆时针旋转 90°至 AB’, 连接B’C,求△AB’C 的面积
(3)拓展提升:如图 3,等边△EBC 中,EC=BC=3cm,点 O 在 BC 上且 OC=2cm,动点 P 从点 E 沿射线EC 以 1cm/s 速度运动,连接 OP,将线段 OP 绕点O 逆时针旋转 120°得到线段 OF,设点 P 运动的时间为t 秒。
当t= 秒时,OF∥ED


若要使点F 恰好落在射线EB 上,求点P 运动的时间t
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习解直角三角形以后,重庆八中数学兴趣小组测量了旗杆的高度.如图,某一时刻,旗杆AB的影子一部分落在平台上的影长BC为6米,落在斜坡上的影长CD为4米,AB⊥BC,同一时刻,光线与旗杆的夹角为37°,斜坡的坡角为30°,旗杆的高度AB约为( )米.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ![]() ≈1.73)
≈1.73)
A.10.61
B.10.52
C.9.87
D.9.37
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com