
【题目】如图,在平面直角坐标系中点A(![]() ,
, ![]() ),B(2
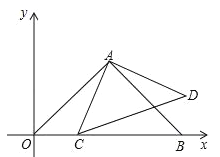
),B(2![]() ,0),点C为线段OB上一个动点,以AC为腰作等腰直角△ACD,且AC=AD.
,0),点C为线段OB上一个动点,以AC为腰作等腰直角△ACD,且AC=AD.
(1)△AOB的面积;
(2)证明:OC2+CB2=CD2.
【答案】(1)S△AOB=3;(2)见解析
【解析】试题分析:(1)根据题意可知A(![]() ,
, ![]() ),B(2
),B(2![]() ,0),利用三角形的面积公式直接求解即可;(2)连接BD,根据题意求得OA=AB=
,0),利用三角形的面积公式直接求解即可;(2)连接BD,根据题意求得OA=AB=![]() ,根据勾股定理的逆定理判定三角形AOB为等腰直角三角形,再利用SAS判定△OAC≌△BAD,根据全等三角形的性质可得OC=BD,,∠AOC=∠ABD=45°,即可得∠CBD=90°,再由勾股定理即可得结论.
,根据勾股定理的逆定理判定三角形AOB为等腰直角三角形,再利用SAS判定△OAC≌△BAD,根据全等三角形的性质可得OC=BD,,∠AOC=∠ABD=45°,即可得∠CBD=90°,再由勾股定理即可得结论.
试题解析:
(1) S△AOB=![]() ×2
×2![]() ×
×![]() =3;
=3;
(2)证明:连接BD,
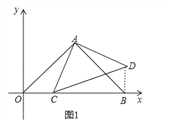
由题意得OA=AB=![]() ,
,
∵OA=AB=![]() ,OB=2
,OB=2![]() ,
,
∴OA2+OB2=OB2,
∴∠OAB=90°,∠AOB=∠ABO=45°,
∵∠OAB=∠CAD,
∴∠OAC=∠BAD,
∵∠AO=AB,AC=AD,
∴△OAC≌△BAD,
∴OC=BD,∠AOC=∠ABD=45°,
∴∠CBD=90°,
∴CD2=BC2+BD2.


科目:初中数学 来源: 题型:
【题目】实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线![]() 射到平面镜
射到平面镜![]() 上,被
上,被![]() 反射到平面镜
反射到平面镜![]() 上,又被
上,又被![]() 反射,若被
反射,若被![]() 反射出的光线
反射出的光线![]() 与光线
与光线![]() 平行,且
平行,且![]() ,则
,则![]() _________,
_________,![]() ________.
________.
(2)在(1)中,若![]() ,则
,则![]() _______;若
_______;若![]() ,则
,则![]() ________;
________;
(3)由(1)、(2),请你猜想:当两平面镜![]() 、
、![]() 的夹角
的夹角![]() ________时,可以使任何射到平面镜
________时,可以使任何射到平面镜![]() 上的光线
上的光线![]() ,经过平面镜
,经过平面镜![]() 、
、![]() 的两次反射后,入射光线
的两次反射后,入射光线![]() 与反射光线
与反射光线![]() 平行.请说明理由.
平行.请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
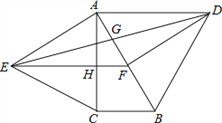
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC; ②四边形ADFE为菱形; ③AD=4AG; ④FH=![]() BD
BD
其中正确的结论有( ).
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC三个顶点的坐标分别为A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+
x2+ ![]() x+3
x+3 ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).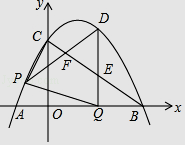
(1)求直线BC的函数表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
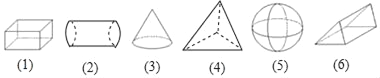
【题目】下列请写出下列几何体,并将其分类.(只填写编号)
如果按“柱”“锥”“球”来分,柱体有_____,椎体有_____,球有_____;
如果按“有无曲面”来分,有曲面的有_____,无曲面的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D在AB上,点E与点C在AB的两侧,连接BE,CD,点M、N分别是BE、CD的中点,连接MN,AM,AN. 下列结论:①△ACD≌△ABE;②△ABC∽△AMN;③△AMN是等边三角形;④若点D是AB的中点,则S△ABC=2S△ABE .
其中正确的结论是 . (填写所有正确结论的序号)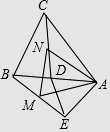
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件. ①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com