
在△ABC中,∠BAC=45°,AD⊥BC于D,将△ABD沿AB所在的直线折叠,使点D落在点E处;将△ACD沿AC所在的直线折叠,使点D落在点F处,分别延长EB、FC使其交于点M.
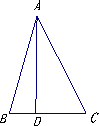
(1)判断四边形AEMF的形状,并给予证明.
(2)若BD=1,CD=2,试求四边形AEMF的面积.
|
解:(1)∵AD △AEB是由△ADB折叠所得 ∴∠1=∠3,∠E=∠ADB= AE=AD 又∵△AFC是由△ADC折叠所得 ∴∠2=∠4,∠F=∠ADC= ∴AE=AF 2分 又∵∠1+∠2= ∴∠3+∠4= ∴∠EAF= ∴四边形AEMF是正方形. 5分
(2)方法一:设正方形AEMF的边长为x 根据题意知:BE=BD,CF=CD ∴BM=x-1; CM=x-2 7分 在Rt△BMC中,由勾股定理得: ∴ 解之得: ∴ 方法二:设:AD=x ∴ ∴ ∵ 且 ∴ 解之得: ∴ |


科目:初中数学 来源: 题型:
 ;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.
;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.| S△BCQ |
| S△ABC |
| 1 |
| 3 |
| S△BPQ |
| S△ABC |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以4cm/s的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从点A出发,沿AB以每秒4cm,的速度向点B运动,同时点Q从C点出发,沿CA以3cm/s的速度向点A运动,设运动时间为x秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com