
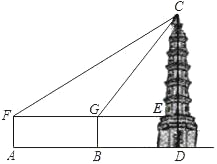
【题目】计算:在一次数学社团活动课上,同学们测量一座古塔CD的高度,他们首先在A处安置测量器,测得塔顶C的仰角∠CFE=30°,然后往塔的方向前进100米到达B处,此时测得塔顶C的仰角∠CGE=60°,已知测量器高1.5米,请你根据以上数据计算出古塔CD的高度.(保留根号)
科目:初中数学 来源: 题型:
【题目】(8分)如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE.
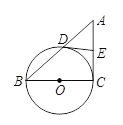
(1)若AD=DB,OC=5,求切线AC的长.
(2)求证:ED是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°.
(1)作出经过点B,圆心O在斜边AB上且与边AC相切于点E的⊙O(要求:用尺规作图,保留作图痕迹,不写作法和证明)
(2)设(1)中所作的⊙O与边AB交于异于点B的另外一点D,若⊙O的直径为5,BC=4;求DE的长.(如果用尺规作图画不出图形,可画出草图完成(2)问)

查看答案和解析>>
科目:初中数学 来源: 题型:
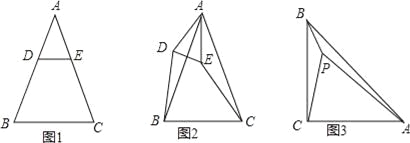
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10![]() 海里,求AC的距离.(结果保留根号)
海里,求AC的距离.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是方程x2﹣(k﹣2)x+k2+3k+5=0的两个实数根,则x12+x22的最大值是( )
A. 19 B. 18 C. 15 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
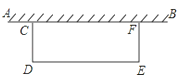
【题目】如图,有一段15m长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用32m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为126m2的长方形场地?
(2)长方形场地面积能达到130m2吗?如果能,请给出设计方案,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图,若双曲线![]() (k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线
(k>0)与它的其中一条对称轴y=x相交于两点A,B,则线段AB的长称为双曲线![]() (k>0)的对径.
(k>0)的对径.

(1)求双曲线![]() 的对径;
的对径;
(2)若某双曲线![]() (k>0)的对径是
(k>0)的对径是![]() .求k的值.
.求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com