
|
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,直线DA切⊙O于A,AB是⊙O的一条直径,点C是⊙O上异于A、B的任一点,则下列结论不一定正确的是( )
如图,直线DA切⊙O于A,AB是⊙O的一条直径,点C是⊙O上异于A、B的任一点,则下列结论不一定正确的是( )A、∠CAB=
| ||
| B、AD∥OC | ||
| C、AD2=DC•DB | ||
| D、AB⊥AD |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 成本(元/件) | 56 | 58 | 60 | 62 | 64 | 66 | 68 |
查看答案和解析>>
科目:初中数学 来源: 题型:
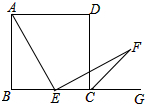 如图,在正方形ABCD中,边长AB=3,点E(与B,C不重合)是BC边上任意一点,把EA绕点E顺时针方向旋转90°到EF,连接CF.
如图,在正方形ABCD中,边长AB=3,点E(与B,C不重合)是BC边上任意一点,把EA绕点E顺时针方向旋转90°到EF,连接CF.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
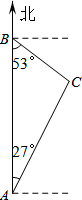 如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.
如图,禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为99海里,可疑船只正沿南偏东53°方向航行.我渔政船迅速沿北偏东27°方向前去拦截,2小时后刚好在C处将可疑船只拦截.求该可疑船只航行的速度.| 9 |
| 20 |
| 9 |
| 10 |
| 1 |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com