
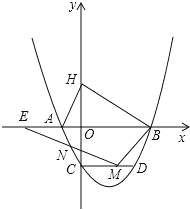
【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(4,0),与y轴交于C(0,﹣2).
(1)求抛物线的解析式;
(2)H是C关于x轴的对称点,P是抛物线上的一点,当△PBH与△AOC相似时,求符合条件的P点的坐标(求出两点即可);
(3)过点C作CD∥AB,CD交抛物线于点D,点M是线段CD上的一动点,作直线MN与线段AC交于点N,与x轴交于点E,且∠BME=∠BDC,当CN的值最大时,求点E的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)P的坐标为(﹣1,0)或(8,18);(3)E的坐标为(﹣
x﹣2;(2)P的坐标为(﹣1,0)或(8,18);(3)E的坐标为(﹣![]() ,0).
,0).
【解析】
试题分析:(1)由抛物线与x轴交于A(﹣1,0),B(4,0),可设抛物线的解析式为y=a(x+1)(x﹣4),然后将(0,﹣2)代入解析式即可求出a的值;(2)当△PBH与△AOC相似时,△PBH是直角三角形,由![]() 可知∠AHB=90°,根据待定系数法求出直线AH的解析式后,联立一次函数与二次函数的解析式后即可求出P的坐标;(3)设M的坐标为(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用对应边的比相等即可得出CN与m的函数关系式,利用二次函数的性质即可求出m=
可知∠AHB=90°,根据待定系数法求出直线AH的解析式后,联立一次函数与二次函数的解析式后即可求出P的坐标;(3)设M的坐标为(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用对应边的比相等即可得出CN与m的函数关系式,利用二次函数的性质即可求出m=![]() 时,CN有最大值,然后再证明△EMB∽△BDM,即可求出E的坐标.
时,CN有最大值,然后再证明△EMB∽△BDM,即可求出E的坐标.
试题解析:(1)∵抛物线与x轴交于A(﹣1,0),B(4,0),
∴设抛物线的解析式为:y=a(x+1)(x﹣4),
把(0,﹣2)代入y=a(x+1)(x﹣4),
∴a=![]() ,
,
∴抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)当△PBH与△AOC相似时,
∴△AOC是直角三角形,
∴△PBH也是直角三角形,
由题意知:H(0,2),
∴OH=2,
∵A(﹣1,0),B(4,0),
∴OA=1,OB=4,
∴![]()
∵∠AOH=∠BOH,
∴△AOH∽△BOH,
∴∠AHO=∠HBO,
∴∠AHO+∠BHO=∠HBO+∠BHO=90°,
∴∠AHB=90°,
设直线AH的解析式为:y=kx+b,
把A(﹣1,0)和H(0,2)代入y=kx+b,
∴![]() ,
,
∴解得k=2,b=2,
∴直线AH的解析式为:y=2x+2,
联立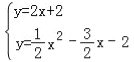 ,
,
解得:x=1或x=﹣8,
当x=﹣1时,
y=0,
当x=8时,
y=18
∴P的坐标为(﹣1,0)或(8,18)
(3)过点M作MF⊥x轴于点F,
设点E的坐标为(n,0),M的坐标为(m,0),
∵∠BME=∠BDC,
∴∠EMC+∠BME=∠BDC+∠MBD,
∴∠EMC=∠MBD,
∵CD∥x轴,
∴D的纵坐标为﹣2,
令y=﹣2代入y=![]() x2﹣
x2﹣![]() x﹣2,
x﹣2,
∴x=0或x=3,
∴D(3,﹣2),
∵B(4,0),
∴由勾股定理可求得:BD=![]() ,
,
∵M(m,0),
∴MD=3﹣m,CM=m(0≤m≤3)
∴由抛物线的对称性可知:∠NCM=∠BDC,
∴△NCM∽△MDB,
∴![]() ,
,
∴![]() ,
,
∴CN=![]() ,
,
∴当m=![]() 时,CN可取得最大值,
时,CN可取得最大值,
∴此时M的坐标为(![]() ,﹣2),
,﹣2),
∴MF=2,BF=![]() ,MD=
,MD=![]()
∴由勾股定理可求得:MB=![]() ,
,
∵E(n,0),
∴EB=4﹣n,
∵CD∥x轴,
∴∠NMC=∠BEM,∠EBM=∠BMD,
∴△EMB∽△BDM,
∴![]() ,
,
∴MB2=MDEB,
∴![]() =
=![]() ×(4﹣n),
×(4﹣n),
∴n=﹣![]() ,
,
∴E的坐标为(﹣![]() ,0).
,0).


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
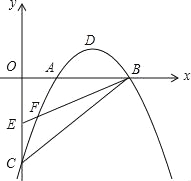
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
(1)(1,0),(6,0),(6,1),(5,0),(6,-1),(6,0);
(2)(2,0),(5,3),(4,0);
(3)(2,0),(5,-3),(4,0).
观察所得到的图形像什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B是反比例函数y=![]() (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为( )
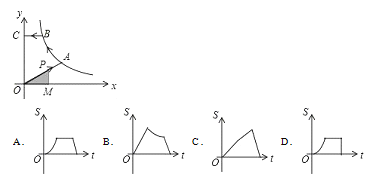
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
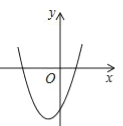
A.y1<y2 B.y1>y2
C.y的最小值是﹣3 D.y的最小值是﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P在x轴上,且点P到y轴的距离为1,则点P的坐标为( )
A. (0,1) B. (1,0)
C. (0,1)或(0,-1) D. (1,0)或(-1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中必然发生的事件是 ( )
A.一个图形旋转后所得的图形与原来的图形不全等
B.100件产品中有4件次品,从中任意抽取5件,至少一件是正品
C.不等式的两边同时乘以一个数,结果仍是不等式
D.随意翻一本书的某页,这页的页码一定是偶数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在所给正方形网格图中完成下列各题:(用直尺画图,保留痕迹)
(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点Q,使QA+QC最小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com