
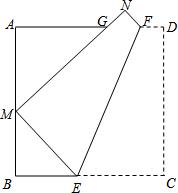
 如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:
如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:分析 (1)根据正方形的性质和折叠的性质得出∠A=∠B,∠AGM=∠BME,再利用相似三角形的判定证明即可;
(2)设BE=x,利用勾股定理得出x的值,再利用相似三角形的性质证明即可;
(3)设BM=x,AM=a-x,利用勾股定理和相似三角形的性质证明即可.
解答 证明:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=90°,
∴∠AMG+∠AGM=90°,
∵EF为折痕,
∴∠GME=∠C=90°,
∴∠AMG+∠BME=90°,
∴∠AGM=∠BME,
在△AGM与△BME中,
∵∠A=∠B,∠AGM=∠BME,
∴△AGM∽△BME;
(2)∵M为AB中点,
∴BM=AM=$\frac{a}{2}$,
设BE=x,则ME=CE=a-x,
在Rt△BME中,∠B=90°,
∴BM2+BE2=ME2,即($\frac{a}{2}$)2+x2=(a-x)2,
∴x=$\frac{3}{8}$a,
∴BE=$\frac{3}{8}$a,ME=$\frac{5}{8}$a,
由(1)知,△AGM∽△BME,
∴$\frac{AG}{BM}$=$\frac{GM}{ME}$=$\frac{AM}{BE}$=$\frac{4}{3}$,
∴AG=$\frac{4}{3}$BM=$\frac{2}{3}$a,GM=$\frac{4}{3}$ME=$\frac{5}{6}$a,
∴$\frac{AM}{3}$=$\frac{AG}{4}$=$\frac{MG}{5}$;
(3)设BM=x,则AM=a-x,ME=CE=a-BE,
在Rt△BME中,∠B=90°,
∴BM2+BE2=ME2,即x2+BE2=(a-BE)2,
解得:BE=$\frac{a}{2}$-$\frac{x2}{2a}$,
由(1)知,△AGM∽△BME,
∴$\frac{C△AGM}{C△BME}$=$\frac{AM}{BE}$=$\frac{2a}{a+x}$,
∵C△BME=BM+BE+ME=BM+BE+CE=BM+BC=a+x,
∴C△AGM=C△BME•$\frac{AM}{BE}$=(a+x)•$\frac{2a}{a+x}$=2a.
点评 此题考查了折叠的性质、正方形的性质、勾股定理以及相似三角形的判定与性质.此题难度较大,注意掌握数形结合思想与方程思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,甲、乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字.游戏规定:转动两个转盘停止后,指针所指的两个数字之积为奇数时,甲获胜;为偶数时,乙获胜.
如图所示,甲、乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字.游戏规定:转动两个转盘停止后,指针所指的两个数字之积为奇数时,甲获胜;为偶数时,乙获胜.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<c<b | B. | b<a<c | C. | c<b<a | D. | a<b<c |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com