
【题目】如图,抛物线y1=a(x+2)2﹣3与y2= ![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论: ①无论x取何值,y2的值总是正数;
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论: ①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4;
④2AB=3AC;
其中正确结论是( )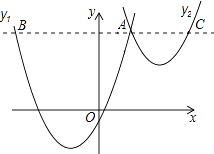
A.①②
B.②③
C.③④
D.①④
【答案】D
【解析】解:①∵抛物线y2= ![]() (x﹣3)2+1开口向上,顶点坐标在x轴的上方,∴无论x取何值,y2的值总是正数,故本小题正确; ②把A(1,3)代入,抛物线y1=a(x+2)2﹣3得,3=a(1+2)2﹣3,解得a=
(x﹣3)2+1开口向上,顶点坐标在x轴的上方,∴无论x取何值,y2的值总是正数,故本小题正确; ②把A(1,3)代入,抛物线y1=a(x+2)2﹣3得,3=a(1+2)2﹣3,解得a= ![]() ,故本小题错误;
,故本小题错误;
② 由两函数图象可知,抛物线y1=a(x+2)2﹣3解析式为y1= ![]() (x+2)2﹣3,当x=0时,y1=
(x+2)2﹣3,当x=0时,y1= ![]() (0+2)2﹣3=﹣
(0+2)2﹣3=﹣ ![]() ,y2=
,y2= ![]() (0﹣3)2+1=
(0﹣3)2+1= ![]() ,故y2﹣y1=
,故y2﹣y1= ![]() +
+ ![]() =
= ![]() ,故本小题错误;
,故本小题错误;
③ 物线y1=a(x+2)2﹣3与y2= ![]() (x﹣3)2+1交于点A(1,3),
(x﹣3)2+1交于点A(1,3),
∴y1的对称轴为x=﹣2,y2的对称轴为x=3,
∴B(﹣5,3),C(5,3)
∴AB=6,AC=4,
∴2AB=3AC,故本小题正确.
故选D.
根据与y2= ![]() (x﹣3)2+1的图象在x轴上方即可得出y2的取值范围;把A(1,3)代入抛物线y1=a(x+2)2﹣3即可得出a的值;由抛物线与y轴的交点求出,y2﹣y1的值;根据两函数的解析式直接得出AB与AC的关系即可.
(x﹣3)2+1的图象在x轴上方即可得出y2的取值范围;把A(1,3)代入抛物线y1=a(x+2)2﹣3即可得出a的值;由抛物线与y轴的交点求出,y2﹣y1的值;根据两函数的解析式直接得出AB与AC的关系即可.


科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x﹣2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2﹣3x+1和y2=ax2+bx+c,若y1﹣y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当﹣3≤x≤3时,y2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,小明和小芳从同一小区门口同时出发,沿同一路线去离该小区1800米的少年宫参加活动,为响应“节能环保,绿色出行”的号召,两人都步行,已知小明的速度是小芳的速度的1.2倍,结果小明比小芳早6分钟到达,求小芳的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E. 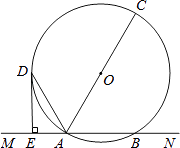
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
(3)在(2)的条件下,直接写出tan∠CAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,点P从点A开始,沿AB边以1cm/s的速度向点B运动:点Q从点B开始,沿BC边以2cm/s的速度向点C运动,当点P运动到点B时,运动停止,如果P,Q分别从A,B两点同时出发. 
(1)几秒后△PBQ的面积等于8cm2?
(2)几秒后以P,B,Q为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF. 求证:直线BE是⊙O的切线.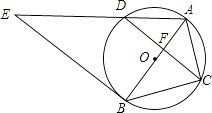
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点O,F为BC的中点,连接EF,DF,DE,则下列结论:①EF=DF;②ADAC=AEAB;③△DOE∽△COB;④若∠ABC=45°时,BE= ![]() FC. 其中正确的是(把所有正确结论的序号都选上)
FC. 其中正确的是(把所有正确结论的序号都选上)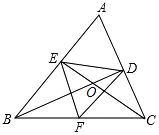
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com