
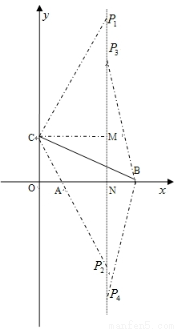
(本题12分)如图,在平面直角坐标系中,已知OA=2,OC=4,⊙M与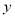 轴相切于点C,与
轴相切于点C,与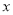 轴交于A,B两点,∠ACD=90°,抛物线
轴交于A,B两点,∠ACD=90°,抛物线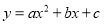 经过A,B,C三点.
经过A,B,C三点.
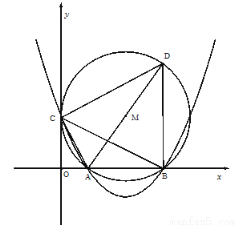
(1)求证:∠CAO=∠CAD;
(2)求弦BD的长;
(3)在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.
(1)证明详见解析;(2)8;(3)存在,符合条件的点P有四个,坐标分别为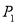
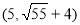 ,
,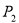
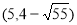 ,
,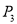
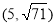 ,
,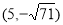 .
.
【解析】
试题分析:(1)利用切线的性质得出∠MCO=90°,进而得出∠OCA=∠MCD=∠MDC,再利用∠OCA+∠OAC=90°求出即可;
(2)利用圆周角定理以及平行线的性质,首先得出四边形COMN为矩形,进而求出BD=2MN;
(3)分别利用当CP=CB时,△PCB为等腰三角形,当BP=BC时,△PCB为等腰三角形,利用勾股定理求出即可.
试题解析:(1)证明:如图,连接MC,
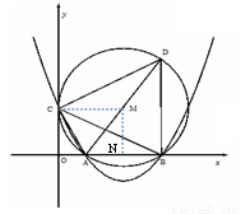
∵⊙M与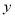 轴相切于点C,∴CM⊥OC,
轴相切于点C,∴CM⊥OC,
∴∠MCO=90°,
又∵∠ACD=90°,
∴AD为⊙M的直径,
∵DM=CM, ∠ACD+∠ADC=90°,
∴∠MCD=∠MDC,
∵∠OCA+∠ACM=∠OCM=90°,
∴∠MCD+∠ACM=90°,
∴∠OCA=∠MCD=∠MDC,
∵∠OCA+∠OAC=90°,
∴∠OAC=∠CAD;
(2)【解析】
如图,过点M作MN⊥OB于点N,
由(1)可知,AD是⊙M的直径,
∴∠ABD=90°,
∵MN⊥AB, ∴∠MNA=90°,
∴MN∥BD,
∴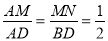 ,
,
∵∠OCM=∠CON=∠MNO=90°,
∴四边形COMN为矩形,
∴MN=CO=4,
∴BD=2MN=8;
(3)【解析】
抛物线的对称轴上存在点P,使ΔPBC是以BC为腰的等腰三角形.
在⊙M中,弧AC=弧AC,∴∠ADC=∠ABC,
由(1)知,∠ADC=∠OCA,
∴∠OCA=∠OBC,
在Rt△CAO和Rt△BOC中,tan∠OCA=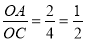 ,
,
∴tan∠OBC=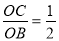 ,
,
∴OB=2OC=8,
∴A(2,0),B(8,0),
∵抛物线经过A,B两点,
∴A,B关于抛物线的对称轴对称,其对称轴为直线: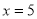 ;
;
当CP=CB=5时,△PCB为等腰三角形,
在Rt△COB中, ,
,
如图,在Rt△CM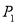 中,
中,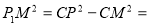 80-25=55,
80-25=55,
∴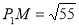 ,
,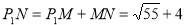
∴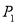
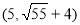 ,
,
同理可求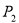 的坐标是
的坐标是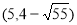 ,
,
当BP=BC=5时,△PCB为等腰三角形, ,
,
∴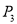
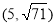 ,
,
同理可得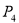 坐标为
坐标为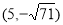 ,
,
∴符合条件的点P有四个,坐标分别为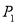
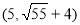 ,
,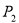
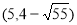 ,
,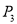
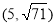 ,
,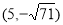 .
.
考点:二次函数综合题.
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


科目:初中数学 来源:2014-2015学年四川省巴中市平昌县九年级下学期第一次综合性阶段考试数学试卷(解析版) 题型:解答题
(12分)如图,抛物线y = ax2 + bx + 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
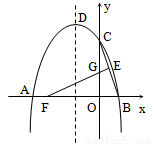
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长及H点的坐标;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,△EFK的面积最大?并求出最大面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省巴中市平昌县九年级下学期第一次综合性阶段考试数学试卷(解析版) 题型:填空题
已知x、y为实数,且 +(y+2)2=0,则yx= .
+(y+2)2=0,则yx= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省巴中市平昌县九年级下学期第一次综合性阶段考试数学试卷(解析版) 题型:选择题
要使 有意义,则x应满足( ).
有意义,则x应满足( ).
A.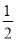 ≤x≤3 B.x≤3且x≠
≤x≤3 B.x≤3且x≠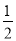 C.
C.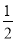 <x<3 D.
<x<3 D.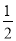 <x≤3
<x≤3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省枣庄市九年级3月测试数学试卷(解析版) 题型:解答题
(本题6分)如图所示,在⊙O中,  =
=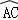 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.

(1)求证:AC2=ABAF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省学业水平模拟考试数学试卷(解析版) 题型:解答题
(本小题满分8分)有3张不透明的卡片,除正面写有不同的数字外,其它均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的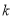 ,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的
,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的 .
.

(1)写出 为负数的概率;
为负数的概率;
(2)求一次函数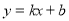 的图象经过二、三、四象限的概率。(用树状图或列表法求解)
的图象经过二、三、四象限的概率。(用树状图或列表法求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com