
【题目】如图,在矩形ABCD中,DE平分∠ADC, 且∠EDO=15°,则∠OED=________°.
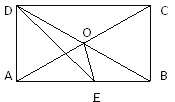
【答案】30
【解析】在矩形ABCD中,∠ADC=90°,DE平分∠ADC,则∠ADE=∠CDE=45°,
又∠EDO=15°,则∠ADO=∠ADE+∠EDO=60°,在矩形ABCD中,对角线AC与BD相等且互相平分,AO=DO,又∠ADO=60°,得△ADO是等边三角形,AO=DO=AD,
∠AOD=∠DAO=∠ADO=60°,又∠DAE=90°,∠ADE=45°,△ADE是等腰直角三角形,AD=AE,∠AED=∠ADE=45°,∴AO=AD=AE,△EAO是等腰三角形,∠AOE=∠AEO,
又∠EAO=90°-∠DAO=30°,得∠AEO=(180°-∠EAO)/2=75°,
∠OED=∠AEO-∠AED=75°-45°=30°,故答案为:30.


科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后回答问题:
解方程: ![]()
解:①当![]() ≥0时,原方程可化为:
≥0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
②当![]() <0时,原方程可化为:
<0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
所以原方程的解是![]() 或
或![]()
(1)解方程: ![]()
(2)探究:当![]() 为何值时,方程
为何值时,方程![]() ①无解;②只有一个解;③有两个解。
①无解;②只有一个解;③有两个解。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE. 
(1)求证:DE是⊙O的切线.
(2)填空: ①当∠CAB=时,四边形AOED是平行四边形;
②连接OD,在①的条件下探索四边形OBED的形状为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E,分别取BC,DE的中点M,N,连接MN.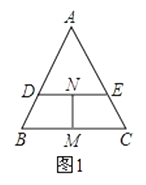
(1)发现:在图1中, ![]() =;
=;
(2)应用:如图2,将△ADE绕点A旋转,请求出 ![]() 的值;
的值;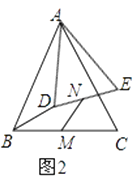
(3)拓展:如图3,△ABC和△ADE是等腰三角形,且∠BAC=∠DAE,M,N分别是底边BC,DE的中点,若BD⊥CE,请直接写出 ![]() 的值.
的值.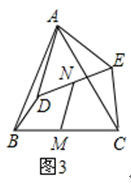
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是4, ![]() 的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则
的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则![]() 的最小值是( )
的最小值是( )

A. 2 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(7,3),点E在边AB上,且AE=1,已知点P为y轴上一动点,连接EP,过点O作直线EP的垂线段,垂足为点H,在点P从点F(0, ![]() )运动到原点O的过程中,点H的运动路径长为 .
)运动到原点O的过程中,点H的运动路径长为 . 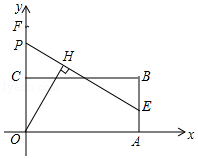
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.求: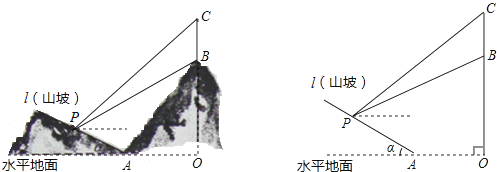
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的三条角平分线相交于点O,过点O作EF∥BC,分别交AB于E,交AC于F,则图中的等腰△有( )个

(A)4(B)5
(C)6(D)7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,直线![]() ,另一直线交
,另一直线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,且
,且![]() ,点
,点![]() 为直线
为直线![]() 上一动点,点
上一动点,点![]() 为直线
为直线![]() 上一动点,且
上一动点,且![]() .
.
(![]() )如图
)如图![]() ,当点
,当点![]() 在点
在点![]() 右边且点
右边且点![]() 在点
在点![]() 左边时,
左边时,![]() 的平分线交
的平分线交![]() 的平分线于点
的平分线于点![]() ,求
,求![]() 的度数;
的度数;
(![]() )如图
)如图![]() ,当点
,当点![]() 在点
在点![]() 右边且点
右边且点![]() 在点
在点![]() 右边时,
右边时,![]() 的平分线交
的平分线交![]() 的平分线于点
的平分线于点![]() ,求
,求![]() 的度数;
的度数;
(![]() )当点
)当点![]() 在点
在点![]() 左边且点
左边且点![]() 在点
在点![]() 左边时,
左边时,![]() 的平分线交
的平分线交![]() 的平分线所在直线交于点
的平分线所在直线交于点![]() ,请直接写出
,请直接写出![]() 的度数,不说明理由.
的度数,不说明理由.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com