
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
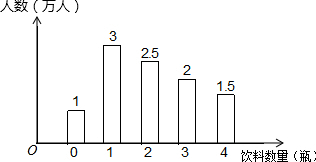 某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图
某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况,一天,他们分别在A、B、C三个出口处,对离开园区的游客进行调查,其中在A出口调查所得的数据整理后绘成图| 出 口 | B | C |
| 人均购买饮料数量(瓶) | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
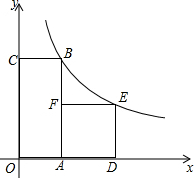 如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.
如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半釉上,点F在AB上,点B、E在反比例函数$y=\frac{k}{x}$的图象上OA=1,OC=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=100}\\{2x+4y=350}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=100}\\{4x+2y=350}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x-y=100}\\{4x+2y=350}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=100}\\{2x+4y=350}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图中,利用面积的等量关系验证的公式是( )
如图中,利用面积的等量关系验证的公式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+2b)(a-b)=a2+ab-2b2 | D. | (a+b)2=a2+2ab+b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com