练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】南洞庭大桥是南益高速公路上的重要桥梁，小芳同学在校外实践活动中对此开展测量活动．如图，在桥外一点A测得大桥主架与水面的交汇点C的俯角为α，大桥主架的顶端D的仰角为β，已知测量点与大桥主架的水平距离AB＝a，则此时大桥主架顶端离水面的高CD为( )

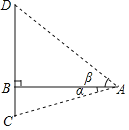
    A.asinα+asinβB.acosα+acosβC.atanα+atanβD.

    【答案】C

    【解析】

    在Rt△ABD和Rt△ABC中，由三角函数得出BC＝atanα，BD＝atanβ，得出CD＝BC+BD＝atanα+atanβ即可．

    在Rt△ABD和Rt△ABC中，AB＝a，tanα＝，tanβ＝，

    ∴BC＝atanα，BD＝atanβ，

    ∴CD＝BC+BD＝atanα+atanβ，

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

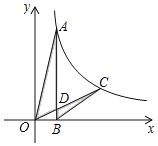
    【题目】如图，已知点A，点C在反比例函数y＝（k＞0，x＞0）的图象上，AB⊥x轴于点B，OC交AB于点D，若CD＝OD，则△AOD与△BCD的面积比为__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如下图1，将三角板放在正方形上，使三角板的直角顶点与正方形的顶点重合，三角板的一边交于点．另一边交的延长线于点．

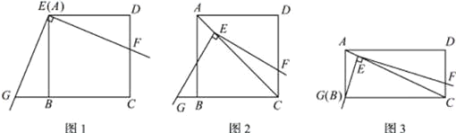
    （1）观察猜想：线段与线段的数量关系是 ；

    （2）探究证明：如图2，移动三角板，使顶点始终在正方形的对角线上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：

    （3）拓展延伸：如图3，将（2）中的“正方形”改为“矩形”，且使三角板的一边经过点，其他条件不变，若、，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

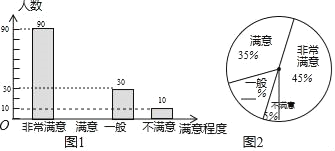
    【题目】为了解市民对全市创文工作的满意程度，娄星区某中学数学兴趣小组在娄底城区范围内进行了抽样调查，将调查结果分为非常满意，满意，一般，不满意四类，回收、整理好全部问卷后，绘制了两幅不完整的统计图1、图2，结合图中信息，回答：

    （1）此次共调查了多少名市民？

    （2）将两幅统计图中不完整的部分补充完整；

    （3）若我市城区共有480000人口，请估算我市对创文工作“非常满意和满意”的市民人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为上标保障我国海外维和部队官兵的生活，现需通过A港口、B港口分别运送100吨和50吨生活物资．已知该物资在甲仓库存有80吨，乙仓库存有70吨，若从甲、乙两仓库运送物资到港口的费用（元/吨）如表所示：

    （1）设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；

    （2）求出最低费用，并说明费用最低时的调配方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y＝x2+（2m﹣1）x﹣2m（m＞0.5）的最低点的纵坐标为﹣4．

    （1）求抛物线的解析式；

    （2）如图1，抛物线与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，D为抛物线上的一点，BD平分四边形ABCD的面积，求点D的坐标；

    （3）如图2，平移抛物线y＝x2+（2m﹣1）x﹣2m，使其顶点为坐标原点，直线y＝﹣2上有一动点P，过点P作两条直线，分别与抛物线有唯一的公共点E、F（直线PE、PF不与y轴平行），求证：直线EF恒过某一定点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y＝x2+bx的对称轴为x＝1，若关于x的一元二次方程x2+bx﹣t＝0（为实数）在﹣1＜x＜4的范围内有解，则t的取值范围是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

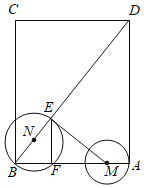
    【题目】如图，在矩形ABCD中，AB＝3，BC＝4，半径为1的动圆圆心M从A点出发，沿着AB方向以1个单位长度/每秒的速度匀速运动，同时动点N从点B出发，沿着BD方向也以1个单位长度/每秒的速度匀速运动，设运动的时间为t秒（0≤t≤2.5），以点N为圆心，NB的长为半径的⊙N与BD，AB的交点分别为E，F，连结EF，ME．

    （1）①当t＝　 　秒时，⊙N恰好经过点M；②在运动过程中，当⊙M与△ABD的边相切时，t＝　 　秒；

    （2）当⊙M经过点B时，①求N到AD的距离；②求⊙N被AD截得的弦长；

    （3）若⊙N与线段ME只有一个公共点时，直接写出t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

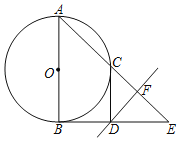
    【题目】如图，在Rt△ABE中，∠B＝90°，以AB为直径的⊙O交AE于点C，CE的垂直平分线FD交BE于点D，连接CD．

    （1）判断CD与⊙O的位置关系，并证明；

    （2）若AC＝6，CE＝8，求⊙O的半径．

    查看答案和解析>>

    同步练习册答案