
【题目】如图1,平面内有一点![]() 到
到![]() 的三个顶点的距离分别为
的三个顶点的距离分别为![]() 若有
若有![]() ,则称点
,则称点![]() 为
为![]() 关于点
关于点![]() 的勾股点.
的勾股点.
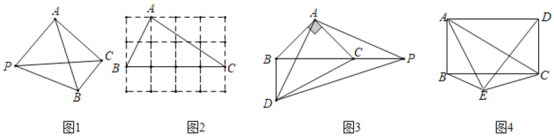
![]() 如图2,在
如图2,在![]() 的方格纸中,每个小正方形的边长均为
的方格纸中,每个小正方形的边长均为![]() 的顶点在格点上,请找出所有的格点
的顶点在格点上,请找出所有的格点![]() ,使点
,使点![]() 为
为![]() 关于点
关于点![]() 的勾股点;
的勾股点;
![]() 如图3,
如图3, ![]() 为等腰直角三角形,
为等腰直角三角形,![]() 是斜边
是斜边![]() 延长线上一点,连接
延长线上一点,连接![]() ,以
,以![]() 为直角边作等腰直角三角形
为直角边作等腰直角三角形 ![]() (点
(点![]() 顺时针排列),
顺时针排列),![]() ,连接
,连接 ![]() 求证:点
求证:点![]() 为
为![]() 关于点
关于点![]() 的勾股点;
的勾股点;
![]() 如图4,点
如图4,点![]() 是矩形
是矩形![]() 外一点,且点
外一点,且点![]() 是
是![]() 关于点
关于点![]() 的勾股点,若
的勾股点,若![]() ,求
,求![]() 的长.
的长.
【答案】![]() 见解析;
见解析;![]() 见解析;
见解析;![]()
![]()
【解析】
(1)如图1,图2,求出PA2,PB2,PC2,得到PC2+PB2=PA2,即得出点P是△ABC关于点A的勾股点;
(2)证明△ABD≌△ACP(SAS),得出BD=CP,∠ABD=∠ACP=135°,证明∠DBP=90°,则结论得证;
(3)由条件“点C是△ABE关于点A的勾股点”可得CE=CD=5,如图3,过点E作MN⊥AB于点M,交DC的延长线于点N,设AM=DN=x,则CN=DN-CD=x-5,由勾股定理可得62-x2=52-(x-5)2,解得:x=![]() ,则求出AM,ME的长,则答案可得出.
,则求出AM,ME的长,则答案可得出.
(1)如图1,
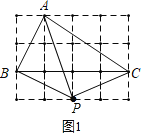
∵PA2=12+32=10,PB2=12+22=5,PC2=PB2=5,
∴PA2=PC2+PB2,
∴点P是△ABC关于点A的勾股点;
如图2,
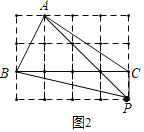
∵PA2=32+32=18,PB2=12+42=17,PC2=1,
∴PA2=PC2+PB2,
∴点P是△ABC关于点A的勾股点;
(2)∵△ABC和△APD为等腰直角三角形,
∴AB=AC,AD=AP,∠BAC=∠DAP=90°,
∴∠BAC-∠DAC=∠DAP-∠DAC,
即∠BAD=∠CAP,
∴△ABD≌△ACP(SAS),
∴BD=PC,∠ABD=∠ACP=135°,
∵∠ABC=45°,
∴∠DBP=∠ABD-∠ABC=135°-45°=90°,
∴BD2+PB2=PD2,
∴PC2+PB2=PD2,
∴点P为△BDC关于点D的勾股点.
(3)解:∵矩形ABCD中,AD=8,
∴AD=BC=8,CD=AB,
∵AD=DE,
∴DE=8,
∵点C是△ABE关于点A的勾股点,
∴AC2=CB2+CE2,
∵AC2=AB2+BC2,
∴CE=CD=5,
如图3,过点E作MN⊥AB于点M,交DC的延长线于点N,
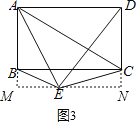
∴∠AME=∠MND=90°,
∴四边形AMND是矩形,
∴MN=AD=8,AM=DN,
设AM=DN=x,则CN=DN-CD=x-5,
∵Rt△DEN中,EN2+DN2=DE2;Rt△CEN中,EN2+CN2=CE2,
∴DE2-DN2=CE2-CN2,
∴62-x2=52-(x-5)2
解得:x=![]() ,
,
∴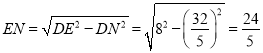 ,
,![]() ,
,
∴![]() ,
,
∴Rt△AME中,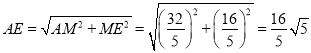 .
.


科目:初中数学 来源: 题型:
【题目】国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出:公民科学素质是实施创新驱动发展战略的基础,是国家综合国力的体现.《方案》明确提出,2020年要将我国公民科学素质的数值提升到10%以上.为了解我国公民科学素质水平及发展状况,中国科协等单位已多次组织了全国范围的调查,以下是根据调查结果整理得到的部分信息.注:科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比.
![]() .2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
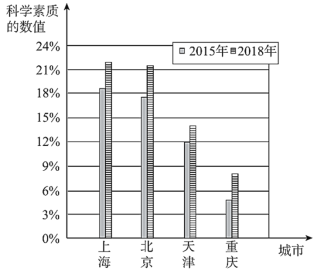
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
2015年 | 2018年 | |
男 |
|
|
女 |
|
|
c.2001年以来我国公民科学素质水平发展统计图如下:
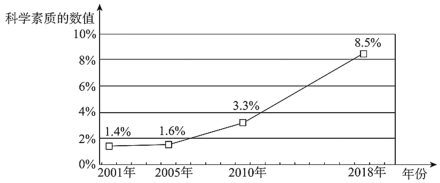
根据以上信息,回答下列问题:
(1)在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是________,公民科学素质水平增速最快的城市是_________.注:科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值;科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值.
(2)已知在2015年的调查样本中,男女公民的比例约为1:1,则2015年我国公民的科学素质水平为______%(结果保留一位小数);由计算可知.在2018年的调查样本中.男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”).
(3)根据截至2018年的调查数据推断,你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象经过点A(0,﹣4)和B(﹣2,2).
(1)求c的值,并用含a的式子表示b;
(2)当﹣2<x<0时,若二次函数满足y随x的增大而减小,求a的取值范围;
(3)直线AB上有一点C(m,5),将点C向右平移4个单位长度,得到点D,若抛物线与线段CD只有一个公共点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=5,BC=4,E是BC边上一点,连接DE,将矩形ABCD沿DE折叠,顶点C恰好落在AB边上点F处,延长DE交AB的延长线于点G.
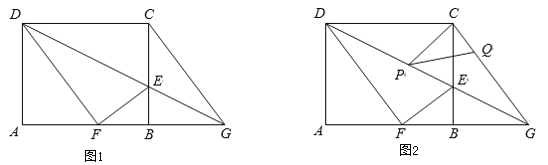
(1)求线段BE的长;
(2)连接CG,求证:四边形CDFG是菱形;
(3)如图2,P,Q分别是线段DG,CG上的动点(与端点不重合),且∠CPQ=∠CDP,是否存在这样的点P,使△CPQ是等腰三角形?若存在,请直接写出DP的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
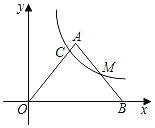
【题目】如图,在平面直角坐标系中,△OAB的边OB在x轴的正半轴上,AO=AB,M是边AB的中点,经过点M的反比例函数y=![]() (k>0,x>0)的图象与边OA交于点C,则
(k>0,x>0)的图象与边OA交于点C,则![]() 的值为__.
的值为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在笔山银子岩坡顶![]() 处的同一水平面上有一座移动信号发射塔
处的同一水平面上有一座移动信号发射塔![]() ,
,
笔山职中数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求:
.求:
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 移动信号发射塔
移动信号发射塔![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C是⊙O上的三个点,点D在BC的延长线上.有如下四个结论:①在∠ABC所对的弧上存在一点E,使得∠BCE=∠DCE;②在∠ABC所对的弧上存在一点E,使得∠BAE=∠AEC;③在∠ABC所对的弧上存在一点E,使得EO平分∠AEC;④在∠ABC所对的弧上任意取一点E(不与点A,C重合) ,∠DCE=∠ABO +∠AEO均成立.上述结论中,所有正确结论的序号是( )

A. ①②③ B. ①③④ C. ②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P是△ABC外部的一定点,D是线段BC上一动点,连接PD交AC于点E.
小明根据学习函数的经验,对线段PD,PE,CD的长度之间的关系进行了探究,
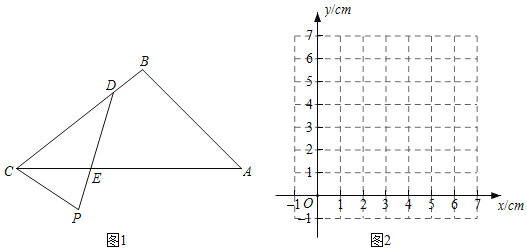
下面是小明的探究过程,请补充完整:
(1)对于点D在BC上的不同位置,画图、测量,得到了线段PD,PE,CD的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
PD/cm | 2.56 | 2.43 | 2.38 | 2.43 | 2.67 | 3.16 | 3.54 | 4.45 | 5.61 |
PE/cm | 2.56 | 2.01 | 1.67 | 1.47 | 1.34 | 1.32 | 1.34 | 1.40 | 1.48 |
CD/cm | 0.00 | 0.45 | 0.93 | 1.40 | 2.11 | 3.00 | 3.54 | 4.68 | 6.00 |
在PD,PE,CD的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出图2中所确定的两个函数的图象;
(3)结合函数图象,解决问题:
连接CP,当△PCD为等腰三角形时,CD的长度约为 cm.(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
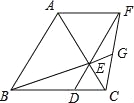
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
【答案】①②③④.
【解析】
试题分析:①由△ABC是等边三角形,可得AB=AC=BC,∠BAC=∠ACB=60°,再因DE=DC,可判定△DEC是等边三角形,所以ED=EC=DC,∠DEC=∠AEF=60°,
因EF=AE,所以△AEF是等边三角形,所以AF=AE,∠EAF=60°,在△ABE和△ACF中,AB=AC,∠BAE=∠CAF,AE=AF ,可判定△ABE≌△ACF,故①正确.②由∠ABC=∠FDC,可得AB∥DF,再因∠EAF=∠ACB=60°,可得AB∥AF,即可判定四边形ABDF是平行四边形,所以DF=AB=BC,故②正确.③由△ABE≌△ACF可得BE=CF,S△ABE=S△AFC,在△BCE和△FDC中,BC=DF,CE=CD,BE=CF ,可判定△BCE≌△FDC,所以S△BCE=S△FDC,即可得S△ABC=S△ABE+S△BCE=S△ACF+S△BCE=S△ABC=S△ACF+S△DCF,故③正确.④由△BCE≌△FDC,可得∠DBE=∠EFG,再由∠BED=∠FEG可判定△BDE∽△FGE,所以![]() =
=![]() ,即
,即![]() =
=![]() ,又因BD=2DC,DC=DE,可得
,又因BD=2DC,DC=DE,可得![]() =2,即FG=2EG.故④正确.
=2,即FG=2EG.故④正确.
考点:三角形综合题.
【题型】填空题
【结束】
19
【题目】先化简,再求值:(a+1-![]() )÷(
)÷(![]() ),其中a=2+
),其中a=2+![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com