
【题目】如图1,在矩形ABCD中,AB=5,BC=4,E是BC边上一点,连接DE,将矩形ABCD沿DE折叠,顶点C恰好落在AB边上点F处,延长DE交AB的延长线于点G.
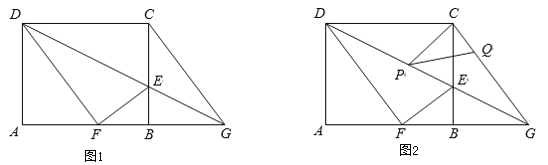
(1)求线段BE的长;
(2)连接CG,求证:四边形CDFG是菱形;
(3)如图2,P,Q分别是线段DG,CG上的动点(与端点不重合),且∠CPQ=∠CDP,是否存在这样的点P,使△CPQ是等腰三角形?若存在,请直接写出DP的值,若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)存在,
;(2)见解析;(3)存在,![]() 或
或![]()
【解析】
(1)设![]() ,由矩形的性质,折叠的性质和勾股定理得出BF,EF的值,然后在
,由矩形的性质,折叠的性质和勾股定理得出BF,EF的值,然后在![]() 中利用勾股定理即可求解;
中利用勾股定理即可求解;
(2)由矩形的性质得出![]() ,然后根据平行线分线段成比例可求出BG的长度,进而可求出FG的长度,则可证明结论;
,然后根据平行线分线段成比例可求出BG的长度,进而可求出FG的长度,则可证明结论;
(3)分两种情况:![]() 和
和![]() ,分别利用等腰三角形的性质和相似三角形的判定及性质得出PG的长度,然后利用勾股定理求出DG的长度,最后利用
,分别利用等腰三角形的性质和相似三角形的判定及性质得出PG的长度,然后利用勾股定理求出DG的长度,最后利用![]() 即可求解.
即可求解.
(1)∵四边形ABCD是矩形,
∴![]() .
.
由折叠的性质可知,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ;
;
(2)证明:![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
 ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
∴四边形CDFG是平行四边形.
∵![]() ,
,
∴四边形CDFG是菱形;
(3)存在,理由如下:
①若![]() ,
,
∵四边形CDFG是菱形,
∴![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ;
;
②若![]() ,
,
过点P作![]() 交CG于点H,
交CG于点H,
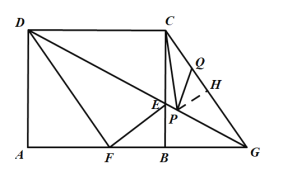
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
∵四边形CDFG是菱形,
∴![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
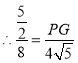 ,
,
![]() ,
,
![]() ,
,
综上所述,DP的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中,对于任意的实数
中,对于任意的实数![]() ,直线
,直线![]() 都经过平面内一个定点
都经过平面内一个定点![]() .
.
(1)求点![]() 的坐标.
的坐标.
(2)反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() 和另外一点
和另外一点![]()
①求![]() 的值;
的值;
②当![]() 时,求
时,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠QAN为锐角,H、B分别为射线AN上的点,点H关于射线AQ的对称点为C,连接AC,CB.
(1)依题意补全图;
(2)CB的垂直平分线交AQ于点E,交BC于点F.连接CE,HE,EB.
①求证:△EHB是等腰三角形;
②若AC+AB=![]() AE,求
AE,求![]() 的值.
的值.
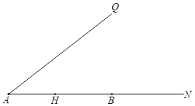
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABC=60°,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接DF.
(1)求证:△ABF是等边三角形;
(2)若∠CDF=45°,CF=2,求AB的长度.
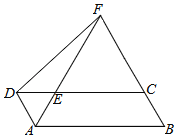
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B是⊙C上的两个点,点P在⊙C的内部.若∠APB为直角,则称∠APB为AB关于⊙C的内直角,特别地,当圆心C在∠APB边(含顶点)上时,称∠APB为AB关于⊙C的最佳内直角.如图1,∠AMB是AB关于⊙C的内直角,∠ANB是AB关于⊙C的最佳内直角.在平面直角坐标系xOy中.
(1)如图2,⊙O的半径为5,A(0,﹣5),B(4,3)是⊙O上两点.
①已知P1(1,0),P2(0,3),P3(﹣2,1),在∠AP1B,∠AP2B,∠AP3B,中,是AB关于⊙O的内直角的是 ;
②若在直线y=2x+b上存在一点P,使得∠APB是AB关于⊙O的内直角,求b的取值范围.
(2)点E是以T(t,0)为圆心,4为半径的圆上一个动点,⊙T与x轴交于点D(点D在点T的右边).现有点M(1,0),N(0,n),对于线段MN上每一点H,都存在点T,使∠DHE是DE关于⊙T的最佳内直角,请直接写出n的最大值,以及n取得最大值时t的取值范围.
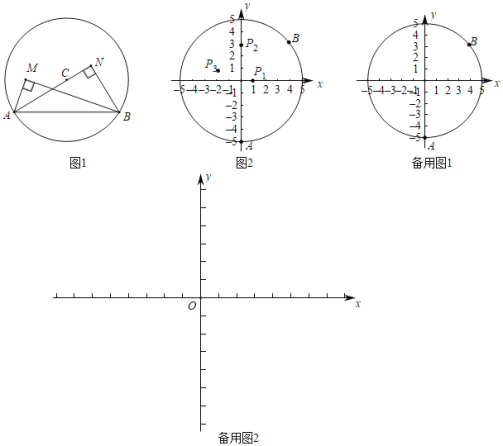
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次综合社会实践活动中,小东同学从A处出发,要到A地北偏东60°方向的C处,他先沿正东方向走了4千米到达B处,再沿北偏东15°方向走,恰能到达目的地C,如图所示,则A、C两地相距__千米.(结果精确到0.1千米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
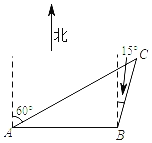
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点![]() 到
到![]() 的三个顶点的距离分别为
的三个顶点的距离分别为![]() 若有
若有![]() ,则称点
,则称点![]() 为
为![]() 关于点
关于点![]() 的勾股点.
的勾股点.
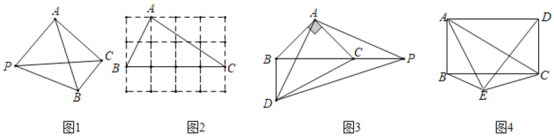
![]() 如图2,在
如图2,在![]() 的方格纸中,每个小正方形的边长均为
的方格纸中,每个小正方形的边长均为![]() 的顶点在格点上,请找出所有的格点
的顶点在格点上,请找出所有的格点![]() ,使点
,使点![]() 为
为![]() 关于点
关于点![]() 的勾股点;
的勾股点;
![]() 如图3,
如图3, ![]() 为等腰直角三角形,
为等腰直角三角形,![]() 是斜边
是斜边![]() 延长线上一点,连接
延长线上一点,连接![]() ,以
,以![]() 为直角边作等腰直角三角形
为直角边作等腰直角三角形 ![]() (点
(点![]() 顺时针排列),
顺时针排列),![]() ,连接
,连接 ![]() 求证:点
求证:点![]() 为
为![]() 关于点
关于点![]() 的勾股点;
的勾股点;
![]() 如图4,点
如图4,点![]() 是矩形
是矩形![]() 外一点,且点
外一点,且点![]() 是
是![]() 关于点
关于点![]() 的勾股点,若
的勾股点,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
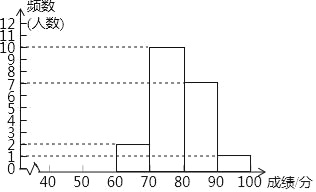
【题目】为了推动全社会自觉尊法学法守法用法,促进全面依法治国,某区每年都举办普法知识竞赛,该区某单位甲、乙两个部门各有员工200人,要在这两个部门中挑选一个部门代表单位参加今年的竞赛,为了解这两个部门员工对法律知识的掌握情况,进行了抽样调查,从甲、乙两个部门各随机抽取20名员工,进行了法律知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息.
a.甲部门成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)
b.乙部门成绩如下:
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.甲、乙两部门成绩的平均数、方差、中位数如下:
平均数 | 方差 | 中位数 | |
甲 | 79.6 | 36.84 | 78.5 |
乙 | 77 | 147.2 | m |
d.近五年该单位参赛员工进入复赛的出线成绩如下:
2014年 | 2015年 | 2016年 | 2017年 | 2018年 | |
出线成绩(百分制) | 79 | 81 | 80 | 81 | 82 |
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)可以推断出选择 部门参赛更好,理由为 ;
(3)预估(2)中部门今年参赛进入复赛的人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的![]() 天数据,整理后绘制成统计表进行分析.
天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨) |
|
|
|
|
| 合计 |
频数 | 1 | 2 |
| 3 |
| |
频率 | 0.05 | 0.10 |
| 0.15 | 1 |
表中![]() 组的频率
组的频率![]() 满足
满足![]() .
.
下面有四个推断:
①表中![]() 的值为20;
的值为20;
②表中![]() 的值可以为7;
的值可以为7;
③这![]() 天的日均可回收物回收量的中位数在
天的日均可回收物回收量的中位数在![]() 组;
组;
④这![]() 天的日均可回收物回收量的平均数不低于3.
天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①②B.①③C.②③④D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com