
����Ŀ�������������������ʵ����������������Դ������Ҫ;�����ֶΣ�Ϊ�˽�2019��ij�еڶ������վ��ɻ��������������������ȡ����2019��ڶ����ȵ�![]() �����ݣ���������Ƴ�ͳ�Ʊ����з�����
�����ݣ���������Ƴ�ͳ�Ʊ����з�����
�վ��ɻ������������ǧ�֣� |
|
|
|
|
| �ϼ� |
Ƶ�� | 1 | 2 |
| 3 |
| |
Ƶ�� | 0.05 | 0.10 |
| 0.15 | 1 |
����![]() ���Ƶ��
���Ƶ��![]() ����
����![]() ��
��
�������ĸ��ƶϣ�
�ٱ���![]() ��ֵΪ20��
��ֵΪ20��
�ڱ���![]() ��ֵ����Ϊ7��
��ֵ����Ϊ7��
����![]() ����վ��ɻ��������������λ����
����վ��ɻ��������������λ����![]() �飻
�飻
����![]() ����վ��ɻ������������ƽ����������3��
����վ��ɻ������������ƽ����������3��
���к����ƶϵ�����ǣ� ��
A.�٢�B.�٢�C.�ڢۢ�D.�٢ۢ�
���𰸡�D
��������
�ٸ��������ܺ�=Ƶ����Ƶ�ʣ���ʽ���㼴�ɵó�m��ֵ��
�ڸ���![]() ��Ƶ��a����
��Ƶ��a����![]() ��������÷�Χ��Ƶ������һ���ó�b��ֵ�ķ�Χ���Ӷ���⣻
��������÷�Χ��Ƶ������һ���ó�b��ֵ�ķ�Χ���Ӷ���⣻
�۸�����λ���Ķ��弴����⣻
�ܸ��ݼ�Ȩƽ�����ļ��㹫ʽ�������.
�⣺���վ��ɻ������������ǧ�֣�Ϊ![]() ʱ��Ƶ��Ϊ1��Ƶ��Ϊ0.05����������m=
ʱ��Ƶ��Ϊ1��Ƶ��Ϊ0.05����������m=![]() ���ƶϺ�����
���ƶϺ�����
��20��0.2=4��20��0.3=6��
1+2+6+3=12���ʱ���b��ֵ����Ϊ7���Dz��������ƶϣ�
��1+2+6=9������m����վ��ɻ��������������λ����![]() �飬�Ǻ����ƶϣ�
�飬�Ǻ����ƶϣ�
�ܣ�1+5����2=3��0.05+0.10=0.15����![]() ����վ��ɻ������������ƽ����������3���Ǻ����ƶ�.
����վ��ɻ������������ƽ����������3���Ǻ����ƶ�.
��ѡ��D


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У�AB=5��BC=4��E��BC����һ�㣬����DE��������ABCD��DE�۵�������Cǡ������AB���ϵ�F�����ӳ�DE��AB���ӳ����ڵ�G��
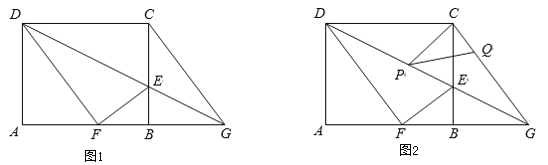
��1�����߶�BE�ij���
��2������CG����֤���ı���CDFG�����Σ�
��3����ͼ2��P��Q�ֱ����߶�DG��CG�ϵĶ��㣨��˵㲻�غϣ����ҡ�CPQ=��CDP���Ƿ���������ĵ�P��ʹ��CPQ�ǵ��������Σ������ڣ���ֱ��д��DP��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��P�ǡ�ABC�ⲿ��һ���㣬D���߶�BC��һ���㣬����PD��AC�ڵ�E��
С������ѧϰ�����ľ��飬���߶�PD��PE��CD�ij���֮��Ĺ�ϵ������̽����
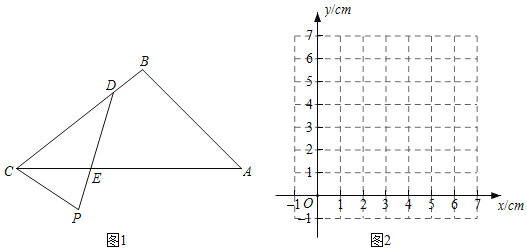
������С����̽�����̣��벹��������
��1�����ڵ�D��BC�ϵIJ�ͬλ�ã���ͼ���������õ����߶�PD��PE��CD�ij��ȵļ���ֵ�������
�1 | �2 | �3 | �4 | �5 | �6 | �7 | �8 | �9 | |
PD/cm | 2.56 | 2.43 | 2.38 | 2.43 | 2.67 | 3.16 | 3.54 | 4.45 | 5.61 |
PE/cm | 2.56 | 2.01 | 1.67 | 1.47 | 1.34 | 1.32 | 1.34 | 1.40 | 1.48 |
CD/cm | 0.00 | 0.45 | 0.93 | 1.40 | 2.11 | 3.00 | 3.54 | 4.68 | 6.00 |
��PD��PE��CD�ij������������У�ȷ���� ���ij������Ա������� ���ij��Ⱥ��� ���ij��ȶ�������Ա����ĺ�����
��2����ͬһƽ��ֱ������ϵxOy�У�����ͼ2����ȷ��������������ͼ��
��3����Ϻ���ͼ������⣺
����CP������PCDΪ����������ʱ��CD�ij���ԼΪ�� ��cm������ȷ��0.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�O�а����²�����ͼ��
��1������O��ֱ��AD��
��2���Ե�DΪԲ�ģ�DO��Ϊ�뾶����������O��B��C���㣻
��3������DB��DC��AB��AC��BC��
����������ͼ���̼�����ͼ�Σ������ĸ������д�����ǣ�������
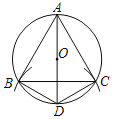
A.��ABD��90��B.��BAD����CBDC.AD��BCD.AC��2CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��2ax��
��1�����κ���ͼ��ĶԳ�����ֱ��x���� ����
��2����0��x��3ʱ��y�����ֵ����Сֵ�IJ�Ϊ4����ö��κ����ı���ʽ��
��3����a��0�����ڶ��κ���ͼ���ϵ�����P��x1��y1����Q��x2��y2������t��x1��t+1��x2��3ʱ��������y1��y2�����Ϻ���ͼ��ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() ��һ�κ���
��һ�κ���![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() �뷴��������
�뷴��������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() ���
���![]() ����
����![]() ��Գƣ�
��Գƣ�
��1��ֱ��д����![]() �����ꣻ
�����ꣻ
��2�����![]() �����꣨�ú�
�����꣨�ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��3����![]() ������ֻ��һ�������߶�
������ֻ��һ�������߶�![]() �ϣ�ֱ��д��
�ϣ�ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�ǵȱ������Σ���D��E�ֱ��ڱ�BC��AC�ϣ���CD=CE������DE���ӳ�����F��ʹEF=AE������AF��CF������BE���ӳ���CF�ڵ�G�����н��ۣ�
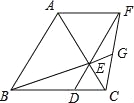
�١�ABE�ա�ACF����BC=DF����S��ABC=S��ACF+S��DCF������BD=2DC����GF=2EG��������ȷ�Ľ����� ������д������ȷ���۵���ţ�
���𰸡��٢ڢۢ�.
��������
���������������ABC�ǵȱ������Σ��ɵ�AB=AC=BC����BAC=��ACB=60�㣬����DE=DC�����ж���DEC�ǵȱ������Σ�����ED=EC=DC����DEC=��AEF=60�㣬
��EF=AE��������AEF�ǵȱ������Σ�����AF=AE����EAF=60�㣬�ڡ�ABE�͡�ACF�У�AB=AC,��BAE=��CAF,AE=AF �����ж���ABE�ա�ACF���ʢ���ȷ��������ABC=��FDC���ɵ�AB��DF��������EAF=��ACB=60�㣬�ɵ�AB��AF�������ж��ı���ABDF��ƽ���ı��Σ�����DF=AB=BC���ʢ���ȷ��������ABE�ա�ACF�ɵ�BE=CF��S��ABE=S��AFC���ڡ�BCE�͡�FDC�У�BC=DF,CE=CD,BE=CF �����ж���BCE�ա�FDC������S��BCE=S��FDC�����ɵ�S��ABC=S��ABE+S��BCE=S��ACF+S��BCE=S��ABC=S��ACF+S��DCF���ʢ���ȷ��������BCE�ա�FDC���ɵ���DBE=��EFG��������BED=��FEG���ж���BDE�ס�FGE������![]() =
=![]() ����
����![]() =
=![]() ������BD=2DC��DC=DE���ɵ�
������BD=2DC��DC=DE���ɵ�![]() =2����FG=2EG���ʢ���ȷ��
=2����FG=2EG���ʢ���ȷ��
���㣺�������ۺ���.
�����͡������
��������
19
����Ŀ���Ȼ�������ֵ��(a��1��![]() )��(
)��(![]() )������a��2��
)������a��2��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
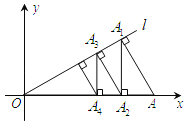
����Ŀ����ͼ������![]() ��ֱ��
��ֱ��![]() �Ĵ��ߣ�����Ϊ��
�Ĵ��ߣ�����Ϊ��![]() ������
������![]() ��
��![]() �ᣬ����Ϊ��
�ᣬ����Ϊ��![]() ������
������![]() ��
��![]() ��������
������Ϊ��![]() ��������������ȥ���õ�һ���߶�
��������������ȥ���õ�һ���߶�![]() �������߶�
�������߶�![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�����ı���![]() �У�
�У�![]()
![]() ����
����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���������˶����ٶ�Ϊ��ͬʱ
���������˶����ٶ�Ϊ��ͬʱ![]() ����
����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ������
������![]() ���ӳ����������˶����ٶ�Ϊ
���ӳ����������˶����ٶ�Ϊ![]() ������
������![]() �����
�����![]() ʱ����
ʱ����![]() ֹͣ�˶�������
ֹͣ�˶�������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() �����˶�ʱ��Ϊ
�����˶�ʱ��Ϊ![]() ������������⣺
������������⣺
![]() ����
����![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]()
![]() ���ı���
���ı���![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
![]() ���˶������У��Ƿ����ijһʱ��
���˶������У��Ƿ����ijһʱ��![]() ��ʹ�ı���
��ʹ�ı���![]() �����Ϊ�ı���
�����Ϊ�ı���![]() �����
�����![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
![]() ���˶������У��Ƿ����ijһʱ��
���˶������У��Ƿ����ijһʱ��![]() �� ʹ
�� ʹ![]() �����ڣ����
�����ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com