
【题目】已知:如图,在四边形![]() 中,
中,![]()
![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为;同时
方向匀速运动,速度为;同时![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向在
方向在![]() 的延长线上匀速运动,速度为
的延长线上匀速运动,速度为![]() ;当点
;当点![]() 到达点
到达点![]() 时,点
时,点![]() 停止运动.过点
停止运动.过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .连接
.连接![]() .设运动时间为
.设运动时间为![]() ,解答下列问题:
,解答下列问题:
![]() 连接
连接![]() ,当
,当![]() 为何值时,
为何值时,![]()
![]() 设四边形
设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 在运动过程中,是否存在某一时刻
在运动过程中,是否存在某一时刻![]() ,使四边形
,使四边形![]() 的面积为四边形
的面积为四边形![]() 面积的
面积的![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
![]() 在运动过程中,是否存在某一时刻
在运动过程中,是否存在某一时刻![]() , 使
, 使![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

【答案】(1)当![]() 为
为![]() 时,
时,![]() (2)
(2)![]() ;(3)当
;(3)当![]() 时,四边形
时,四边形![]() 的面积为四边形
的面积为四边形![]() 面积的
面积的![]() ;(4)当
;(4)当![]() 为
为![]() 时,
时,![]()
【解析】
(1)若![]() ,易得四边形
,易得四边形![]() 是平行四边形,用含t的代数式表示AP和DQ的长度,根据平行四边形的性质得AP=DQ,列方程求解即可.
是平行四边形,用含t的代数式表示AP和DQ的长度,根据平行四边形的性质得AP=DQ,列方程求解即可.
(2)过点![]() 作
作![]() 垂足为
垂足为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .则四边形
.则四边形![]() 是矩形,求得BF=4,AF=6,DF=8,MN=8,由PE∥BD得
是矩形,求得BF=4,AF=6,DF=8,MN=8,由PE∥BD得![]() ,求得AE=AP=2t,证明
,求得AE=AP=2t,证明![]() ,根据相似三角形的性质得
,根据相似三角形的性质得![]() ,
,![]() ,根据
,根据![]() 代入数据整理即可.
代入数据整理即可.
(3)假设存在某一时刻 ![]() 满足条件,列出方程
满足条件,列出方程![]() 求解即可.
求解即可.
(4)若存在某一时刻![]() ,使
,使![]() ,垂足为
,垂足为![]() ,利用条件证得
,利用条件证得![]() ,得到DE=DQ,代入数据求解即可.
,得到DE=DQ,代入数据求解即可.
解:![]() 若
若![]()
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]()
解得![]()
![]() 当
当![]() 为
为![]() 时,
时,![]()
![]()
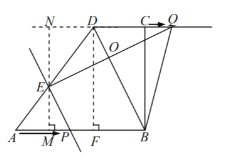
过点![]() 作
作![]() 垂足为
垂足为![]() ,
,
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 与的函数关系式是
与的函数关系式是![]()
![]() 假设存在某一时刻
假设存在某一时刻 ![]() ,
,
四边形![]() 的面积为四边形
的面积为四边形![]() 面积的
面积的![]()
则![]()
解得,![]() (不合题意,舍去)
(不合题意,舍去)
答:当![]() 时,四边形
时,四边形![]() 的面积为四边形
的面积为四边形![]() 面积的
面积的![]()
![]() 若存在某一时刻
若存在某一时刻![]() ,使
,使![]() ,垂足为
,垂足为![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 为
为![]() 时,
时,![]()


科目:初中数学 来源: 题型:
【题目】生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的![]() 天数据,整理后绘制成统计表进行分析.
天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨) |
|
|
|
|
| 合计 |
频数 | 1 | 2 |
| 3 |
| |
频率 | 0.05 | 0.10 |
| 0.15 | 1 |
表中![]() 组的频率
组的频率![]() 满足
满足![]() .
.
下面有四个推断:
①表中![]() 的值为20;
的值为20;
②表中![]() 的值可以为7;
的值可以为7;
③这![]() 天的日均可回收物回收量的中位数在
天的日均可回收物回收量的中位数在![]() 组;
组;
④这![]() 天的日均可回收物回收量的平均数不低于3.
天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①②B.①③C.②③④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级共有80名同学参与数学科托底训练.其中(1)班30人,(2)班25人,(3)班25人,吕老师在托底训练后对这些同学进行测试,并对测试成绩进行整理,得到下面统计图表.
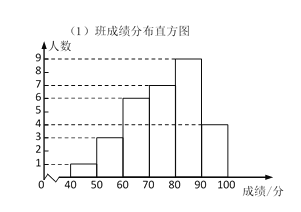
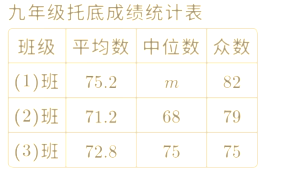
(1)表格中的m落在________组;(填序号)
①40≤x<50, ②50≤x<60, ③60≤x<70,
④70≤x<80, ⑤80≤x<90, ⑥90≤x≤100.
(2)求这80名同学的平均成绩;
(3)在本次测试中,(2)班小颖同学的成绩是70分,(3)班小榕同学的成绩是74分,这两位同学成绩在自己所在班级托底同学中的排名,谁更靠前?请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
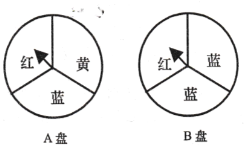
【题目】小颖为班级联欢会设计了一个“配紫色”游戏:如图是两个可以自由转动的转盘,每个转盘被分成面积相等的三个扇形.游戏者同时转动两个转盘,如果一个转盘转出红色,另一个转盘转出蓝色,那么就能配成紫色.小明和小亮参加这个游戏,并约定:若配成紫色,则小明贏;若两个转盘转出的颜色相同,则小亮赢.这个游戏对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
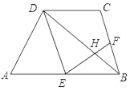
【题目】如图,在四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD交于点H.
(1)求证:四边形DEBC是平行四边形;
(2)若BD=6,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】俄罗斯足球世界杯点燃了同学们对足球运动的热情,某学校划购买甲、乙两种品牌的足球供学生使用.已知用1000 元购买甲种足球的数量和用1600元购买乙种足球的数量相同,甲种足球的单价比乙种足球的单价少30元.
(1)求甲、乙两种品牌的足球的单价各是多少元?
(2)学枝准备一次性购买甲、乙两种品牌的足球共25个,但总费用不超过1610元,那么这所学校最多购买多少个乙种品牌的足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com