练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

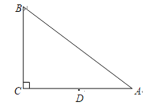
    【题目】如图，在中，，，，点是的中点，点在边上，将沿翻折，使得点落在点处，当时，那么的长为________________．

    【答案】或

    【解析】

    分两种情形分别求解，作DF⊥AB于F，连接AA′．想办法求出AE，利用等腰直角三角形的性质求出AA′即可．

    如图，作DF⊥AB于F，连接AA′．

    在Rt△ACB中，BC＝＝6，

    ∵∠DAF＝∠BAC，∠AFD＝∠C＝90°，

    ∴△AFD∽△ACB，

    ∴，

    ∴，

    ∴DF＝，AF＝，

    ∵A′E⊥AB，

    ∴∠AEA′＝90°，

    由翻折不变性可知：∠AED＝45°，

    ∴EF＝DF＝，

    ∴AE＝A′E＝＋＝，

    ∴AA′＝，

    如图，作DF⊥AB于F，当 EA′⊥AB时，同法可得AE＝＝，AA′＝AE＝．

    故答案为或．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在四边形中，．点从点出发，沿方向匀速运动，速度为；同时，点从点出发，沿方向在的延长线上匀速运动，速度为；当点到达点时，点停止运动．过点作，交于点．连接．设运动时间为，解答下列问题：

    连接，当为何值时，

    设四边形的面积为，求与的函数关系式；

    在运动过程中，是否存在某一时刻，使四边形的面积为四边形面积的，若存在，求出的值；若不存在，请说明理由；

    在运动过程中，是否存在某一时刻， 使若存在，求出的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图(1)，在矩形ABCD中，AD＝nAB，点M，P分别在边AB，AD上(均不与端点重合)，且AP＝nAM，以AP和AM为邻边作矩形AMNP，连接AN，CN.

    （问题发现）

    （1）如图(2)，当n＝1时，BM与PD的数量关系为 ，CN与PD的数量关系为 .

    （类比探究）

    （2）如图(3)，当n＝2时，矩形AMNP绕点A顺时针旋转，连接PD，则CN与PD之间的数量关系是否发生变化？若不变，请就图(3)给出证明；若变化，请写出数量关系，并就图(3)说明理由.

    （拓展延伸）

    （3）在(2)的条件下，已知AD＝4，AP＝2，当矩形AMVP旋转至C，N，M三点共线时，请直接写出线段CN的长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小强每天坚持引体向上锻炼，他记录了某一周每天做引体向上的个数，如下表：

    星期

    日

    一

    二

    三

    四

    五

    六

    个数

    11

    12

    13

    12

    其中有三天的个数墨汁覆盖了，但小强己经计算出这组数据唯一众数是13，平均数是12，那么这组数据的方差是(　　)

    A.B.C.1D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是☉的直径，为☉上一点，是半径上一动点（不与重合），过点作射线，分别交弦，于两点，过点的切线交射线于点．

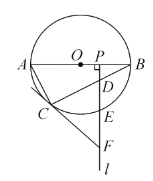
    （1）求证：．

    （2）当是的中点时，

    ①若，判断以为顶点的四边形是什么特殊四边形，并说明理由；

    ②若，且，则_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB//CD，点E是直线AB上的点，过点E的直线l交直线CD于点F，EG平分∠BEF交CD于点G．在直线l绕点E旋转的过程中，图中∠1，∠2的度数可以分别是（ ）

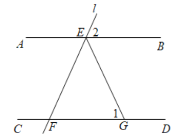
    A.30°，110°B.56°，70°C.70°，40°D.100°，40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，折叠矩形，具体操作：①点为边上一点（不与、重合），把沿所在的直线折叠，点的对称点为点；②过点对折，折痕所在的直线交于点、点的对称点为点．

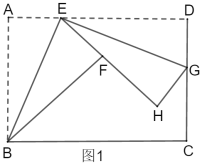
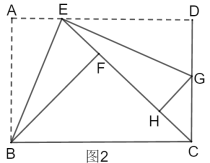
    （1）求证：∽．

    （2）若，．

    ①点在移动的过程中，求的最大值．

    ②如图2，若点恰在直线上，连接，求线段的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数的图象经过点．

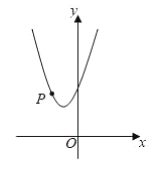
    （1）求的值和图象的顶点坐标；

    （2）点在该二次函数图象上．

    ①当时，求的值；

    ②若点到轴的距离小于2，请根据图象直接写出的取值范围；

    ③直接写出点与直线的距离小于时的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，为测量河岸两灯塔，之间的距离，小明在河对岸处测得灯塔在北偏东方向上，灯塔在东北方向上，小明沿河岸向东行走100米至处，测得此时灯塔在北偏西方向上，已知河两岸．

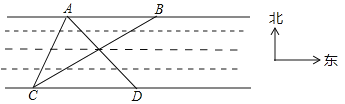
    （1）求观测点到灯塔的距离；

    （2）求灯塔，之间的距离．

    查看答案和解析>>

    同步练习册答案