
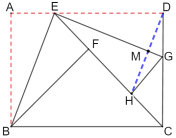
【题目】如图1,折叠矩形![]() ,具体操作:①点
,具体操作:①点![]() 为
为![]() 边上一点(不与
边上一点(不与![]() 、
、![]() 重合),把
重合),把![]() 沿
沿![]() 所在的直线折叠,
所在的直线折叠,![]() 点的对称点为
点的对称点为![]() 点;②过点
点;②过点![]() 对折
对折![]() ,折痕
,折痕![]() 所在的直线交
所在的直线交![]() 于点
于点![]() 、
、![]() 点的对称点为
点的对称点为![]() 点.
点.
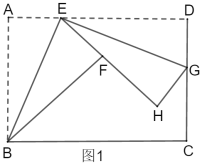
(1)求证:![]() ∽
∽![]() .
.
(2)若![]() ,
,![]() .
.
①点![]() 在移动的过程中,求
在移动的过程中,求![]() 的最大值.
的最大值.
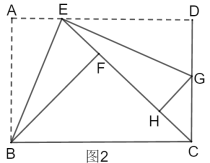
②如图2,若点![]() 恰在直线
恰在直线![]() 上,连接
上,连接![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)①![]() 的最大值为
的最大值为![]() ;②
;②![]()
【解析】
(1)由矩形和折叠的性质可知![]() ,然后通过
,然后通过![]() 得出
得出![]() ,则可证明结论;
,则可证明结论;
(2)设![]() ,则
,则![]() ,根据相似三角形的性质有
,根据相似三角形的性质有![]() ,进而可表示出DG的长度,然后利用二次函数的性质求最大值即可;
,进而可表示出DG的长度,然后利用二次函数的性质求最大值即可;
(3)连接DH,设![]() ,则
,则![]() ,先通过勾股定理求出CF,CE,进而在
,先通过勾股定理求出CF,CE,进而在![]() 中,利用勾股定理求出x的值,进而可求DE,DG,EG的长度,然后利用
中,利用勾股定理求出x的值,进而可求DE,DG,EG的长度,然后利用![]() 求出DM的长度,最后利用
求出DM的长度,最后利用![]() 即可求解.
即可求解.
(1)∵四边形ABCD是矩形,
∴![]() .
.
由折叠的性质可知, ![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ∽
∽![]() ;
;
(2)①设![]() ,则
,则![]() ,
,
由(1)知:![]() ∽
∽![]()
∴![]() ,
,
∴![]() (
(![]() ),
),
故当![]() 时,
时,![]() 取到最大值为
取到最大值为![]() ;
;
②连接DH,
设![]() ,则
,则![]() ,
,
由折叠的性质可知,BF=AB=3,BC=5,
在![]() 中,
中,
![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴DE=4.
由①知:![]() ,
,
∴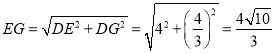 .
.
∵![]() 垂直平分DH,
垂直平分DH,
∴DH=2DM,
又∵![]() ,
,
∴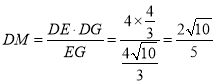 ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
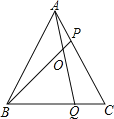
【题目】如图,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O.若BO=6,PO=2,则AP的长,AO的长分别为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳池每次换水前后水的体积基本保持不变,当该游泳池以每小时300立方米的速度放水时,经3小时能将池内的水放完.设放水的速度为x立方米/时,将池内的水放完需y小时.已知该游泳池每小时的最大放水速度为350立方米
(1)求y关于x的函数表达式.
(2)若该游泳池将放水速度控制在每小时200立方米至250立方米(含200立方米和250立方米),求放水时间y的范围.
(3)该游泳池能否在2.5小时内将池内的水放完?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下表
序号 |
| 1 | 2 | … |
① |
| 5 |
| … |
② |
| 2 |
| … |
③ |
|
| 4 | … |
随着![]() 值的逐渐变大,回答下列问题
值的逐渐变大,回答下列问题
(1)当![]() 时,这三个代数式中 的值最小;
时,这三个代数式中 的值最小;
(2)你预计代数式的值最先超过1000的是代数式 ,此时![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育锻炼对学生的健康成长有着深远的影响.某中学 开展了四项球类活动:A:乒乓球;B:足球;C:排球;D:篮球.王老师对学生最喜欢的一项球类活动进行了抽样调查(每人只限一项),并将调查结果绘制成图 1,图2两幅不完整的统计图.
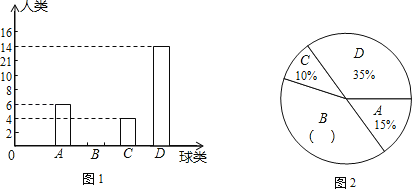
请根据图中信息解答下列问题:
(1)参加此次调查的学生总数是 人;将图1、图2的统计图补充完整;
(2)已知在被调查的最喜欢排球项目的4名学生中只有1名女生,现从这4名学生中任意抽取2名学生参加校排球队,请用列表法或画树状图的方法,求出恰好抽到一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com