
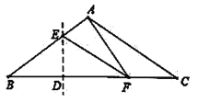
【题目】如图,等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上不与点
上不与点![]() ,
,![]() 重合的一个动点,直线
重合的一个动点,直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,当
,当![]() 是直角三角形时,
是直角三角形时,![]() 的长为______.
的长为______.
【答案】2或![]()
【解析】
分两种情况讨论:
①当∠AFC=90°时,AF⊥BC,利用等腰三角形的三线合一性质和垂直平分线的性质可解;
②当∠CAF=90°时,过点A作AM⊥BC于点M,证明△AMC∽△FAC,列比例式求出FC,从而得BF,再利用垂直平分线的性质得BD.
①当∠AFC=90°时,AF⊥BC,
∵AB=AC,
∴BF=![]() BC=4
BC=4
∵DE垂直平分BF,
∴BD=![]() BF=2;
BF=2;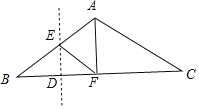
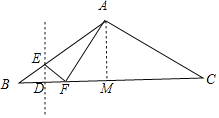
②当∠CAF=90°时,过点A作AM⊥BC于点M,
∵AB=AC,
∴BM=CM,
在Rt△AMC与Rt△FAC中,∠AMC=∠FAC=90°,∠C=∠C,
∴△AMC∽△FAC,
∴![]()
∵AC=10,MC=![]() BC=4,
BC=4,
∴![]()
∴BF=BC-FC=![]()
∴BD=![]() BF=
BF=![]() .
.
故答案为2或![]() .
.


科目:初中数学 来源: 题型:
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() ,类似地,图2所示的算筹图我们可以表述为( )
,类似地,图2所示的算筹图我们可以表述为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x+4与坐标轴交于A,B两点,OC⊥AB于点C,P是线段OC上的一个动点,连接AP,将线段AP绕点A逆时针旋转45°,得到线段AP',连接CP',则线段CP'的最小值为( )
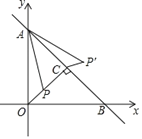
A.![]() B.1C.
B.1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在矩形ABCD中,AD=nAB,点M,P分别在边AB,AD上(均不与端点重合),且AP=nAM,以AP和AM为邻边作矩形AMNP,连接AN,CN.
(问题发现)
(1)如图(2),当n=1时,BM与PD的数量关系为 ,CN与PD的数量关系为 .
(类比探究)
(2)如图(3),当n=2时,矩形AMNP绕点A顺时针旋转,连接PD,则CN与PD之间的数量关系是否发生变化?若不变,请就图(3)给出证明;若变化,请写出数量关系,并就图(3)说明理由.
(拓展延伸)
(3)在(2)的条件下,已知AD=4,AP=2,当矩形AMVP旋转至C,N,M三点共线时,请直接写出线段CN的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长.(参考数据:![]() ≈1.7,结果保留一位小数)
≈1.7,结果保留一位小数)
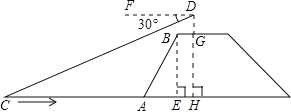
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
个数 | 11 | 12 | 13 | 12 |
其中有三天的个数墨汁覆盖了,但小强己经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
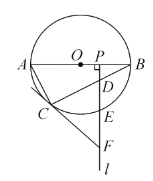
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,折叠矩形![]() ,具体操作:①点
,具体操作:①点![]() 为
为![]() 边上一点(不与
边上一点(不与![]() 、
、![]() 重合),把
重合),把![]() 沿
沿![]() 所在的直线折叠,
所在的直线折叠,![]() 点的对称点为
点的对称点为![]() 点;②过点
点;②过点![]() 对折
对折![]() ,折痕
,折痕![]() 所在的直线交
所在的直线交![]() 于点
于点![]() 、
、![]() 点的对称点为
点的对称点为![]() 点.
点.
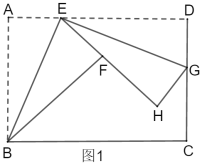
(1)求证:![]() ∽
∽![]() .
.
(2)若![]() ,
,![]() .
.
①点![]() 在移动的过程中,求
在移动的过程中,求![]() 的最大值.
的最大值.
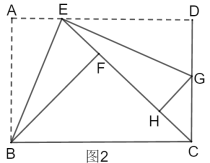
②如图2,若点![]() 恰在直线
恰在直线![]() 上,连接
上,连接![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点 经过点A(﹣1,0),B(5,﹣6),C(6,0)
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com