
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
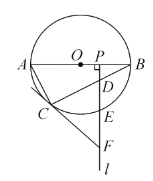
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
【答案】(1)详见解析;(2)①以![]() 为顶点的四边形是菱形;②9
为顶点的四边形是菱形;②9
【解析】
(1)连接OC,根据切线的性质得出OC⊥CF以及∠OBC=∠OCB得∠FCD=∠FDC,可证得结论;
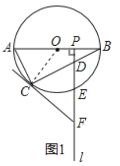
(2)①如图2,连接OC,OE,BE,CE,可证△BOE,△OCE均为等边三角形,可得OB=BE=CE=OC,可得结论;
②设AC=3k,BC=4k(k>0),由勾股定理可求k=6,可得AC=18,BC=24,由面积法可求PE,由勾股定理可求OP的长.
(1)证明:如图1,连接![]() ,则
,则![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() .
.
(2)解:如图2,连接![]() 与
与![]() 交于点
交于点![]() .
.

①以![]() 为顶点的四边形是菱形.理由如下:
为顶点的四边形是菱形.理由如下:
![]() 是直径,
是直径,
![]() .
.
![]() ,
,
![]() .
.
![]() 是
是![]() 的中点,
的中点,
![]() .
.
又![]() ,
,
![]() 均为等边三角形,
均为等边三角形,
![]() ,
,
![]() 四边形
四边形![]() 是菱形.
是菱形.
②![]()
![]() 设
设![]() ,则
,则![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() ,即
,即![]() ,
,
解得![]() ,
,
![]() .
.
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,即
,即![]() ,解得
,解得![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() .
.
故答案为:9.


科目:初中数学 来源: 题型:
【题目】为了维护每个学生平等接受教育的权利,我区小学多年来遵照“就近划片入学”原则实行阳光招生,电脑随机分班,分班时对所有学生一视同仁.小红和小兰两个女孩是邻居,今年夏天被划分到城区的同一所小学,这所学校一年级有1班、2班、3班、4班共四个班.下面是分班前两个女孩家长的一段对话:
小红妈妈说:“真希望她俩能分到同一个班.”
小兰妈妈说:“她俩可能分到同一个班,也可能分不到同一个班,所以她俩分到同一个班的可能性是50%.”
请你用所学的知识分析小兰妈妈的说法是否正确,如正确,请说明理由;如不正确请用列表或画树状图的方法求出小红和小兰分到同一个班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司11月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出![]() 部汽车,则该部汽车的进价为
部汽车,则该部汽车的进价为![]() 万元,每多售出
万元,每多售出![]() 部,所有售出的汽车的进价均降低
部,所有售出的汽车的进价均降低![]() 万元/部.月底厂家再根据销售量返利给销售公司:销售量在
万元/部.月底厂家再根据销售量返利给销售公司:销售量在![]() 部以内(含
部以内(含![]() 部),每部返利
部),每部返利![]() 万元;销售量在
万元;销售量在![]() 部以上,每部返利
部以上,每部返利![]() 万元.
万元.
(1)若该公司当月售出![]() 部汽车,则每部汽车的进价为 万元;
部汽车,则每部汽车的进价为 万元;
(2)若汽车的售价为![]() 万元/部,该公司计划当月盈利
万元/部,该公司计划当月盈利![]() 万元,则需售出多少部汽车? (盈利=销售利润+返利)
万元,则需售出多少部汽车? (盈利=销售利润+返利)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 边于点
边于点![]() .以
.以![]() 上一点
上一点![]() 为圆心作
为圆心作![]() ,使
,使![]() 经过点
经过点![]() 和点
和点![]() .
.
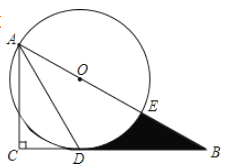
(1)判断直线![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(2)若![]() ,
,![]() .
.
①求![]() 的半径;
的半径;
②设![]() 与
与![]() 边的另一个交点为
边的另一个交点为![]() ,求线段
,求线段![]() ,
,![]() 与劣弧
与劣弧![]() 所围成的阴影部分的面积.(结果保留根号和
所围成的阴影部分的面积.(结果保留根号和![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC约为多少米?( sin42°≈0.7,tan42°≈0.9)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰直角三角形OAB中,∠OAB=90°,OA=AB,点D为OA中点,DC⊥OB,垂足为C,连接BD,点M为线段BD中点,连接AM、CM,如图①.

(1)求证:AM=CM;
(2)将图①中的△OCD绕点O逆时针旋转90°,连接BD,点M为线段BD中点,连接AM、CM、OM,如图②.
①求证:AM=CM,AM⊥CM;
②若AB=4,求△AOM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
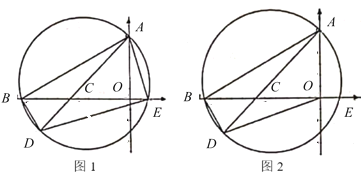
【题目】如图1,在平面直角坐标系中,已知点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,点
,点![]() 为
为![]() 轴正半轴上的一个动点,过点
轴正半轴上的一个动点,过点![]() 、
、![]() 、
、![]() 作
作![]() 的外接圆
的外接圆![]() ,连结
,连结![]() 并延长交圆于点
并延长交圆于点![]() ,连结
,连结![]() 、
、![]() .
.
(1)求证:![]() .
.
(2)当![]() 时,求
时,求![]() 的长度.
的长度.
(3)如图2,连结![]() ,求线段
,求线段![]() 的最小值及当
的最小值及当![]() 最小时
最小时![]() 的外接圆圆心
的外接圆圆心![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
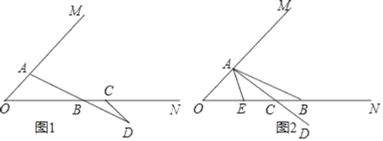
【题目】已知:∠MON=45°,点A在OM上,点B、C在ON上,且OB>OA,
(1)如图1,当点C在点B的右侧时,在ON下方作∠NCD=45°,交AB的延长线于点D.
①若AB=BD,请直接写出线段OA和CD的关系 ;
②若AB=![]() BD,判断线段OA和CD的关系,并说明理由;
BD,判断线段OA和CD的关系,并说明理由;
③若AB=10,BD=8,OB=14,则CD= ;
(2)如图2,当点C在点B的左侧时,在ON下方作∠NCD=45°,CD的反向延长线交AB于点A,在∠OAB的内部作∠BAE=45°,交ON于点E,则线段OE、EB、CB之间的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A,B为反比例函数y=![]() (k>0,x>0)上的两个动点,以A,B为顶点构造菱形ABCD.
(k>0,x>0)上的两个动点,以A,B为顶点构造菱形ABCD.
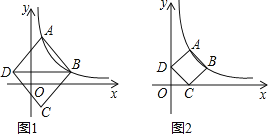
(1)如图1,点A,B横坐标分别为1,4,对角线BD∥x轴,菱形ABCD面积为![]() ,求k的值.
,求k的值.
(2)如图2,当点A,B运动至某一时刻,点C,点D恰好落在x轴和y轴正半轴上,此时∠ABC=90°,求点A,B的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com