
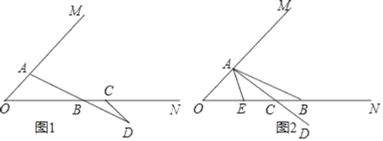
【题目】已知:∠MON=45°,点A在OM上,点B、C在ON上,且OB>OA,
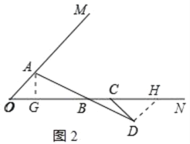
(1)如图1,当点C在点B的右侧时,在ON下方作∠NCD=45°,交AB的延长线于点D.
①若AB=BD,请直接写出线段OA和CD的关系 ;
②若AB=![]() BD,判断线段OA和CD的关系,并说明理由;
BD,判断线段OA和CD的关系,并说明理由;
③若AB=10,BD=8,OB=14,则CD= ;
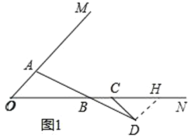
(2)如图2,当点C在点B的左侧时,在ON下方作∠NCD=45°,CD的反向延长线交AB于点A,在∠OAB的内部作∠BAE=45°,交ON于点E,则线段OE、EB、CB之间的数量关系是 .
【答案】(1)①OA=CD,OA⊥CD;②OA=![]() CD,OA⊥CD,见解析;③
CD,OA⊥CD,见解析;③![]() ;(2) EB2=OE2+CB2
;(2) EB2=OE2+CB2
【解析】
(1)①作DH∥OA交ON于H,通过证明△AOB≌△DHB(AAS),可得OA=HD,再通过等边对等角和三角形内角和定理可得CD=HD,∠CDH=90°,即可得OA=CD,CD⊥DH,再根据OA∥DH,即可得证OA⊥CD;②作DH∥OA交ON于H,通过证明△AOB∽△HDB,可得OA=![]() HD,再根据等边对等角和三角形内角和定理可得CD=HD,∠CDH=90°,即可得OA=
HD,再根据等边对等角和三角形内角和定理可得CD=HD,∠CDH=90°,即可得OA=![]() CD,CD⊥DH,再根据OA∥DH,即可得证OA⊥CD;③作DH∥OA交ON于H,作AG⊥OB于G,再根据等腰直角三角形的性质、勾股定理、相似三角形的性质求解即可;
CD,CD⊥DH,再根据OA∥DH,即可得证OA⊥CD;③作DH∥OA交ON于H,作AG⊥OB于G,再根据等腰直角三角形的性质、勾股定理、相似三角形的性质求解即可;
(2)根据旋转的性质证明△BAE≌△BAG(SAS),从而可得EB=GB,在Rt△GBC中,由勾股定理得:GB2=CG2+CB2,即可得证EB2=OE2+CB2.
解:(1)①结论:OA=CD,OA⊥CD.理由如下:
作DH∥OA交ON于H.如图1所示:
∵DH∥OA,
∴∠MON=∠BHD=45°,
在△AOB和△DHB中,
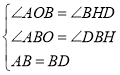 ,
,
∴△AOB≌△DHB(AAS),
∴OA=HD,
∵∠NCD=45°,
∴∠NCD=∠BHD=45°,
∴CD=HD,∠CDH=90°,
∴OA=CD,CD⊥DH,
∵OA∥DH,
∴OA⊥CD;
故答案为:OA=CD,OA⊥CD.
②结论:OA=![]() CD,OA⊥CD.
CD,OA⊥CD.
作DH∥OA交ON于H,如图1所示:
则△AOB∽△HDB,
∴![]() ,
,
∴OA=![]() HD,
HD,
∵∠NCD=∠AOB=∠BHD=45°,
∴CD=HD,∠CDH=90°,
∴OA=![]() CD,CD⊥DH
CD,CD⊥DH
∵OA∥DH,
∴OA⊥CD;
③作DH∥OA交ON于H,作AG⊥OB于G,如图2所示:
则△AOG是等腰直角三角形,
∴AG=OG,在Rt△ABG中,
由勾股定理得:AG2+BG2=AB2,即AG2+(14﹣AG)2=102,
解得:AG=6,或AG=8(舍去),
∴AG=6,
∴OA=![]() AG=6
AG=6![]() ,
,
∵DH∥OA,
∴△AOB∽△HDB,
∴![]() ,即
,即![]() ,
,
解得:HD=![]() ,
,
∵∠NCD=∠AOB=∠BHD=45°,
∴CD=HD=![]() ;
;
故答案为:![]() ;
;
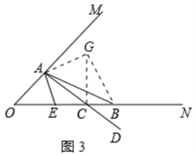
(2)结论:EB2=OE2+CB2.理由如下:
∵∠AOB=∠NCD=∠ACO′=45°,
∴△AOC是等腰直角三角形,
将△AOE绕点A逆时针旋转90°得到△ACG,连接BG,如图3所示:
则∠ACG=∠AOB=45°,AG=AE,CG=OE,
∵∠ACO=∠BCD=45°,
∴∠GCO=45°+45°=90°,
∴∠GCB=90°,
∵∠BAE=45°,∠EAG=90°,
∴∠BAG=45°=∠BAE,
在△BAE和△BAG中,
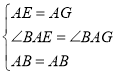
∴△BAE≌△BAG(SAS),
∴EB=GB,
在Rt△GBC中,由勾股定理得:GB2=CG2+CB2,
∴EB2=OE2+CB2.
故答案为:EB2=OE2+CB2.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】如图,灯杆AB与墙MN的距离为18米,小丽在离灯杆(底部)9米的D处测得其影长DE为3m,设小丽身高为1.6m.
(1)求灯杆AB的高度;
(2)小丽再向墙走7米,她的影子能否完全落在地面上?若能,求此时的影长;若不能,求落在墙上的影长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
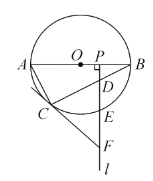
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(﹣4,1),点B的坐标为(﹣1,1).
(1)先将Rt△ABC向右平移5个单位,再向下平移1个单位后得到Rt△A1B1C1.试在图中画出图形Rt△A1B1C1,并写出A1的坐标;
(2)将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出图形Rt△A2B2C2.并计算Rt△A1B1C1在上述旋转过程中C1所经过的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,点D、E分别在边AC、AB上,AD=14,点P是边BC上一动点,当PD+PE的值最小时,AE=15,则BE为( )
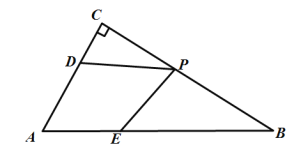
A.30B.29C.28D.27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵黎将中国的清华大学、北京大学及英国的剑桥大学、牛津大学的图片分别贴在4张完全相同的不透明的硬纸板上,制成名校卡片,如图,赵黎将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,洗匀,再随机抽取一张卡片.
(1)赵黎第一次抽取的卡片上的图片是国内大学的概率是多少?
(2)请你用列表法或画树状图法,帮助赵黎求出两次抽取的卡片上的图片一个是国内大学,一个是国外大学的概率.
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗,小红将这五位名人简介分别写在五张完全相同的知识卡片上.
(1)小哲从中随机抽取一张,求卡片上介绍的人物是唐太宗的概率;
(2)用树状图或列表法求小哲从中随机抽取两张,卡片上介绍的人物均是汉朝以后出生的概率.(注:唐太宗、宋太祖、成吉思汗均是汉朝以后出生)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )

A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com