
【题目】某汽车销售公司11月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出![]() 部汽车,则该部汽车的进价为
部汽车,则该部汽车的进价为![]() 万元,每多售出
万元,每多售出![]() 部,所有售出的汽车的进价均降低
部,所有售出的汽车的进价均降低![]() 万元/部.月底厂家再根据销售量返利给销售公司:销售量在
万元/部.月底厂家再根据销售量返利给销售公司:销售量在![]() 部以内(含
部以内(含![]() 部),每部返利
部),每部返利![]() 万元;销售量在
万元;销售量在![]() 部以上,每部返利
部以上,每部返利![]() 万元.
万元.
(1)若该公司当月售出![]() 部汽车,则每部汽车的进价为 万元;
部汽车,则每部汽车的进价为 万元;
(2)若汽车的售价为![]() 万元/部,该公司计划当月盈利
万元/部,该公司计划当月盈利![]() 万元,则需售出多少部汽车? (盈利=销售利润+返利)
万元,则需售出多少部汽车? (盈利=销售利润+返利)
科目:初中数学 来源: 题型:
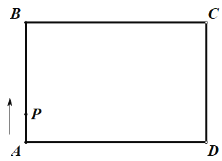
【题目】如图,在矩形![]() 中,点
中,点![]() 从点
从点![]() 出发,沿着矩形的边顺时针方向运动一周回到点
出发,沿着矩形的边顺时针方向运动一周回到点![]() ,则点
,则点![]() 围成的图形面积
围成的图形面积![]() 与点
与点![]() 运动路程
运动路程![]() 之间形成的函数关系式的大致图象是( )
之间形成的函数关系式的大致图象是( )
A.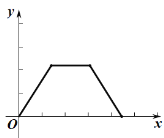 B.
B.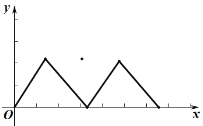
C.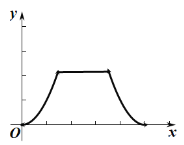 D.
D.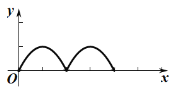
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,灯杆AB与墙MN的距离为18米,小丽在离灯杆(底部)9米的D处测得其影长DE为3m,设小丽身高为1.6m.
(1)求灯杆AB的高度;
(2)小丽再向墙走7米,她的影子能否完全落在地面上?若能,求此时的影长;若不能,求落在墙上的影长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东从![]() 地出发以某一速度向
地出发以某一速度向![]() 地走去,同时小明从
地走去,同时小明从![]() 地出发以另一速度向
地出发以另一速度向![]() 地而行,如图所示,图中的线段
地而行,如图所示,图中的线段![]() 、
、![]() 分别表示小东、小明离
分别表示小东、小明离![]() 地的距离
地的距离![]() 、
、![]() (千米)与所用时间
(千米)与所用时间![]() (小时)的关系.
(小时)的关系.

(1)写出![]() 、
、![]() 与
与![]() 的关系式:_______,_______;
的关系式:_______,_______;
(2)试用文字说明:交点![]() 所表示的实际意义.
所表示的实际意义.
(3)试求出![]() 、
、![]() 两地之间的距离.
两地之间的距离.
(4)求出小东、小明相距4千米时出发的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若平面直角坐标系内的点M满足横、纵坐标都为整数,则把点M叫做“整点”.例如:P(1,0)、Q(2,﹣2)都是“整点”.抛物线y=mx2﹣4mx+4m﹣2(m>0)与x轴交于点A、B两点,若该抛物线在A、B之间的部分与线段AB所围成的区域(包括边界)恰有七个整点,则m的取值范围是( )
A. ![]() ≤m<1B.
≤m<1B. ![]() <m≤1C. 1<m≤2D. 1<m<2
<m≤1C. 1<m≤2D. 1<m<2
查看答案和解析>>
科目:初中数学 来源: 题型:
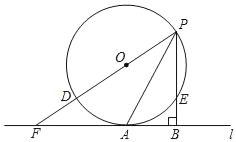
【题目】如图所示,⊙O的半径为4,点A是⊙O上一点,直线l过点A;P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD延长线交直线l于点F,点A是![]() 的中点.
的中点.
(1)求证:直线l是⊙O的切线;
(2)若PA=6,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
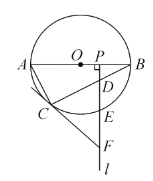
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗,小红将这五位名人简介分别写在五张完全相同的知识卡片上.
(1)小哲从中随机抽取一张,求卡片上介绍的人物是唐太宗的概率;
(2)用树状图或列表法求小哲从中随机抽取两张,卡片上介绍的人物均是汉朝以后出生的概率.(注:唐太宗、宋太祖、成吉思汗均是汉朝以后出生)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com