
����Ŀ��Ϊ��ά��ÿ��ѧ��ƽ�Ƚ��ܽ�����Ȩ��������Сѧ�������������ͽ���Ƭ��ѧ��ԭ��ʵ��������������������ְ࣬�ְ�ʱ������ѧ��һ��ͬ�ʣ�С���С������Ů�����ھӣ��������챻���ֵ�������ͬһ��Сѧ������ѧУһ�꼶��1�ࡢ2�ࡢ3�ࡢ4��ĸ��࣮�����Ƿְ�ǰ����Ů���ҳ���һ�ζԻ���
С������˵������ϣ�������ֵܷ�ͬһ���࣮��
С������˵�����������ֵܷ�ͬһ���࣬Ҳ���ֲܷ���ͬһ���࣬���������ֵ�ͬһ����Ŀ�������50%����
��������ѧ��֪ʶ����С�������˵���Ƿ���ȷ������ȷ����˵�����ɣ��粻��ȷ�����б�����״ͼ�ķ������С���С���ֵ�ͬһ����ĸ��ʣ�
���𰸡�С���������˵������ȷ��![]()
��������
���������б�����״ͼ���ٸ����б�����״ͼ������⼴�ɣ�
�⣺С���������˵������ȷ��
�б����£�
�� | 1�� | 2�� | 3�� | 4�� |
�� | ||||
1�� | ��1�࣬1�ࣩ | ��1�࣬2�ࣩ | ��1�࣬3�ࣩ | ��1�࣬4�ࣩ |
2�� | ��2�࣬1�ࣩ | ��2�࣬2�ࣩ | ��2�࣬3�ࣩ | ��2�࣬4�ࣩ |
3�� | ��3�࣬1�ࣩ | ��3�࣬2�ࣩ | ��3�࣬3�ࣩ | ��3�࣬4�ࣩ |
4�� | ��4�࣬1�ࣩ | ��4�࣬2�ࣩ | ��4�࣬3�ࣩ | ��4�࣬4�ࣩ |
����״ͼ���ԣ���
���б�������״ͼ����֪һ����16�ֿ��ܳ��ֵĽ������ÿ�ֽ�����ֵĿ�������ͬ������С���С���ֵ�ͬһ����Ľ����4�֣�
���ԣ�![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
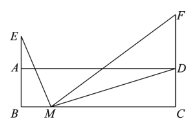
����Ŀ����֪������y��ax2+bx+c(a��0)�Ķ���M(1����4a)���ҹ���A(4��t)����x�ύ��B��C����(��B�ڵ�C�����)��ֱ��l������A��B����y�ύ�ڵ�D.
(1)��a����1����2��x��4ʱ����y�ķ�Χ��
(2)����MBC�ǵ���ֱ�������Σ����ABM�������
(3)��E��ֱ��l�Ϸ����������ϵĶ��㣬��BDE����������ֵΪ![]() ����P�������ߵĶԳ����ϵ�һ�㣬��Q���������ϣ��Ե�A��B��P��QΪ������ı����ܷ�Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵������.
����P�������ߵĶԳ����ϵ�һ�㣬��Q���������ϣ��Ե�A��B��P��QΪ������ı����ܷ�Ϊ���Σ����ܣ������P�����ꣻ�����ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
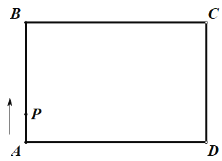
����Ŀ����ͼ���ھ���![]() �У���
�У���![]() �ӵ�
�ӵ�![]() ���������ž��εı�˳ʱ�뷽���˶�һ�ܻص���
���������ž��εı�˳ʱ�뷽���˶�һ�ܻص���![]() �����
�����![]() Χ�ɵ�ͼ�����
Χ�ɵ�ͼ�����![]() ���
���![]() �˶�·��
�˶�·��![]() ֮���γɵĺ�����ϵʽ�Ĵ���ͼ����( )
֮���γɵĺ�����ϵʽ�Ĵ���ͼ����( )
A.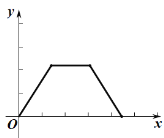 B.
B.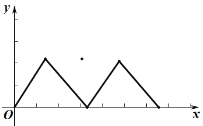
C.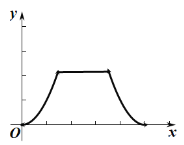 D.
D.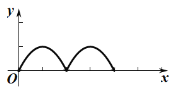
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() �ӳ����ϵĶ��㣬
�ӳ����ϵĶ��㣬![]() Ϊ
Ϊ![]() ���ϵ�һ�����㣬����
���ϵ�һ�����㣬����![]() ��������
��������![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ��������
��������![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
С������ѧϰ�����ľ��飬���߶�![]() �ij���֮��Ĺ�ϵ������̽����
�ij���֮��Ĺ�ϵ������̽����
������С��̽���Ĺ��̣��벹��������
��1�����ڵ�![]() ��
��![]() �ϵIJ�ͬλ�ã���ͼ���������õ����߶�
�ϵIJ�ͬλ�ã���ͼ���������õ����߶�![]() �ij��ȵļ���ֵ�����±���
�ij��ȵļ���ֵ�����±���
�1 | �2 | �3 | �4 | �5 | �6 | �7 | �8 | �9 | |
| 0.00 | 0.53 | 1.00 | 1.69 | 2.17 | 2.96 | 3.46 | 3.79 | 4.00 |
| 0.00 | 1.00 | 1.74 | 2.49 | 2.69 | 2.21 | 1.14 | 0.00 | 1.00 |
| 4.12 | 3.61 | 3.16 | 2.52 | 2.09 | 1.44 | 1.14 | 1.02 | 1.00 |
��![]() �ij������������У�ȷ��_____�ij������Ա�����_____�ij��Ⱥ�_____�ij��ȶ�������Ա����ĺ�����
�ij������������У�ȷ��_____�ij������Ա�����_____�ij��Ⱥ�_____�ij��ȶ�������Ա����ĺ�����
��2����ͬһƽ��ֱ������ϵ![]() �У�������1������ȷ��������������ͼ��
�У�������1������ȷ��������������ͼ��
��3����ϻ����ĺ���ͼ������⣺��![]() ʱ��
ʱ��![]() �ij���ԼΪ________
�ij���ԼΪ________![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ�ּ����ֻ��ܣ�����ṹ��Ϊͼ2���ɿ���![]() ������
������![]() �Ͷ���
�Ͷ���![]() ��ɣ����
��ɣ����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��1�����ֻ��ܵĸߣ���![]() ��
��![]() �ľ��룩��
�ľ��룩��
��2����ͨ������ȷ�����Ϊ![]() ���ֻ��������ֻ������ܷ��е��ڽǶȵĿռ䣮
���ֻ��������ֻ������ܷ��е��ڽǶȵĿռ䣮
���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() �������ȷ��0.1
�������ȷ��0.1![]() ��
��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ���Ҳࣩ����
���Ҳࣩ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ����֪
����֪![]() ��
��![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]() ��
��![]()
��1���������ߵı���ʽ��
��2��һ����![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ��ÿ��1����λ���ȵ��ٶ����
��ÿ��1����λ���ȵ��ٶ����![]() �˶���ͬʱ��
�˶���ͬʱ��![]() �ӵ�
�ӵ�![]() ���������߶�
���������߶�![]() ��ÿ��1����λ���ȵ��ٶ����
��ÿ��1����λ���ȵ��ٶ����![]() �˶�������
�˶�������![]() �˶�����
�˶�����![]() ʱ����
ʱ����![]() ��ֹ֮ͣ�˶������˶�ʱ��Ϊ
��ֹ֮ͣ�˶������˶�ʱ��Ϊ![]() �룬��
�룬��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ���ƣ�
���ƣ�
��3������![]() ��
��![]() ����һ���㣬��
����һ���㣬��![]() ����������һ���㣬���ж��Ƿ�����Ե�
����������һ���㣬���ж��Ƿ�����Ե�![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����
Ϊ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
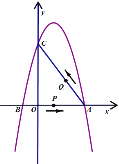
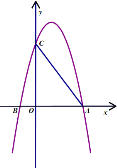


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪BC�ǡ�O��ֱ������D��BC�ӳ�����һ�㣬AB=AD��AE�ǡ�O���ң���AEC=30�㣮
��1����֤��ֱ��AD�ǡ�O�����ߣ�
��2����AE��BC������ΪM����O�İ뾶Ϊ4����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ƹ�AB��ǽMN�ľ���Ϊ18�ף�С������Ƹˣ��ײ���9��D�������Ӱ��DEΪ3m����С������Ϊ1.6m.
��1����Ƹ�AB�ĸ߶ȣ�
��2��С������ǽ��7�ף�����Ӱ���ܷ���ȫ���ڵ����ϣ����ܣ����ʱ��Ӱ���������ܣ�������ǽ�ϵ�Ӱ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ����
����![]() ��ֱ����
��ֱ����![]() Ϊ��
Ϊ��![]() ��һ�㣬
��һ�㣬![]() �ǰ뾶
�ǰ뾶![]() ��һ���㣨����
��һ���㣨����![]() �غϣ�������
�غϣ�������![]() ������
������![]() ���ֱ���
���ֱ���![]() ��
��![]() ��
��![]() ���㣬����
���㣬����![]() �����߽�����
�����߽�����![]() �ڵ�
�ڵ�![]() ��
��
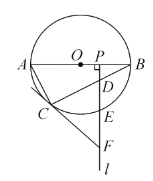
��1����֤��![]() ��
��
��2����![]() ��
��![]() ���е�ʱ��
���е�ʱ��
����![]() �����
���ж���![]() Ϊ������ı�����ʲô�����ı��Σ���˵�����ɣ�
Ϊ������ı�����ʲô�����ı��Σ���˵�����ɣ�
����![]() ����
����![]() ����
����![]() _________��
_________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com