
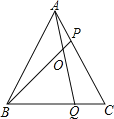
【题目】如图,在等边三角形ABC的AC,BC边上各取一点P,Q,使AP=CQ,AQ,BP相交于点O.若BO=6,PO=2,则AP的长,AO的长分别为__________.
【答案】4,![]() .
.
【解析】
先通过条件证明△ABP≌△ACQ,得到∠ABP=∠CAQ,可证明△APO∽△BPA,得出![]() ,则AP2=OPBP,可求出AP,设OA=x,则AB=2x,在Rt△ABE中,由AE2+BE2=AB2,得出x的值即可得解.
,则AP2=OPBP,可求出AP,设OA=x,则AB=2x,在Rt△ABE中,由AE2+BE2=AB2,得出x的值即可得解.
解:解:∵△ABC是等边三角形
∴∠BAP=∠ACQ=∠ABQ=60°,AB=AC=BC,
∵在△ABP和△ACQ中
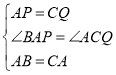 ,
,
∴△ABP≌△ACQ (SAS),
∴∠ABP=∠CAQ,
∵∠APO=∠BPA,
∴△APO∽△BPA,
∴![]() ,
,
∴AP2=OPBP,
∵BO=6,PO=2,
∴BP=8,
∴AP2=2×8=16,
∴AP=4,
∵∠BAC=60°,
∴∠BAQ+∠CAQ=60°,
∴∠BAQ+∠ABP=60°,
∵∠BOQ=∠BAQ+ABP,
∴∠BOQ=60°,
过点B作BE⊥OQ于点E,
∴∠OBE=30°,
∵OB=6,
∴OE=3,BE=3![]() ,
,
∵![]() ,
,
设OA=x,则AB=2x,
在Rt△ABE中,AE2+BE2=AB2,
∴(x+3)2+(3![]() )2=(2x)2,
)2=(2x)2,
解得:x=![]() 或x=1-
或x=1-![]() (舍去),
(舍去),
∴AO=1+![]() .
.
故答案为:4,![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△EDF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
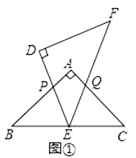
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
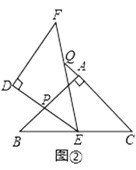
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;
(3)在(2)的条件下,BP=2,CQ=9,则BC的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
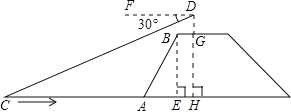
【题目】如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长.(参考数据:![]() ≈1.7,结果保留一位小数)
≈1.7,结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是☉
是☉![]() 的直径,
的直径,![]() 为☉
为☉![]() 上一点,
上一点,![]() 是半径
是半径![]() 上一动点(不与
上一动点(不与![]() 重合),过点
重合),过点![]() 作射线
作射线![]() ,分别交弦
,分别交弦![]() ,
,![]() 于
于![]() 两点,过点
两点,过点![]() 的切线交射线
的切线交射线![]() 于点
于点![]() .
.
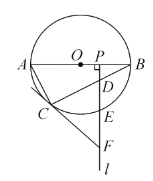
(1)求证:![]() .
.
(2)当![]() 是
是![]() 的中点时,
的中点时,
①若![]() ,判断以
,判断以![]() 为顶点的四边形是什么特殊四边形,并说明理由;
为顶点的四边形是什么特殊四边形,并说明理由;
②若![]() ,且
,且![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
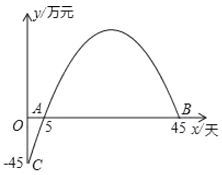
【题目】天然生物制药公司投资制造某药品,先期投入了部分资金.企划部门根据以往经验发现,生产销售中所获总利润![]() 随天数
随天数![]() (可以取分数)的变化图象如下,当总利润到达峰值后会逐渐下降,当利润下降到
(可以取分数)的变化图象如下,当总利润到达峰值后会逐渐下降,当利润下降到![]() 万元时即为止损点,则停止生产
万元时即为止损点,则停止生产
(1)设![]() ,求出最大利润是多少?
,求出最大利润是多少?
(2)在(1)的条件下,经公司研究发现如果添加![]() 名工人
名工人![]() ,在工资成本增加的情况下,总利润关系式变为
,在工资成本增加的情况下,总利润关系式变为![]() ,请研究添加
,请研究添加![]() 名工人后总利润的最大值,并给出总利润最大的方案中的
名工人后总利润的最大值,并给出总利润最大的方案中的![]() 值及生产天数.
值及生产天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
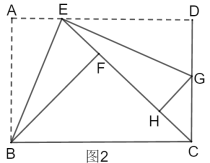
【题目】如图1,折叠矩形![]() ,具体操作:①点
,具体操作:①点![]() 为
为![]() 边上一点(不与
边上一点(不与![]() 、
、![]() 重合),把
重合),把![]() 沿
沿![]() 所在的直线折叠,
所在的直线折叠,![]() 点的对称点为
点的对称点为![]() 点;②过点
点;②过点![]() 对折
对折![]() ,折痕
,折痕![]() 所在的直线交
所在的直线交![]() 于点
于点![]() 、
、![]() 点的对称点为
点的对称点为![]() 点.
点.
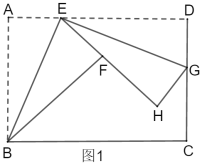
(1)求证:![]() ∽
∽![]() .
.
(2)若![]() ,
,![]() .
.
①点![]() 在移动的过程中,求
在移动的过程中,求![]() 的最大值.
的最大值.
②如图2,若点![]() 恰在直线
恰在直线![]() 上,连接
上,连接![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y=(ax-1)(x-a),其中a是常数,且a≠0.
(1)当a=2时,试判断点(-![]() ,-5)是否在该函数图象上.
,-5)是否在该函数图象上.
(2)若函数的图象经过点(1,-4),求该函数的表达式.
(3)当![]() -1≤x≤
-1≤x≤![]() +1时,y随x的增大而减小,求a的取值范围.
+1时,y随x的增大而减小,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
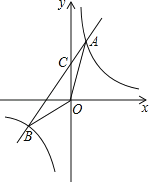
【题目】如图,已知一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
的图象交于A,B两点,点A的横坐标是2,点B的纵坐标是-2.
(1)求一次函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的纸箱里有分别标有汉字“热”“爱”“祖”“国”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先摇匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“国”字的概率;
(2)小红从中任取球,不放回,再从中任取一球,请用树状图或列表法,求小红取出的两个球上的汉字恰好能组成“爱国”或“祖国”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com