
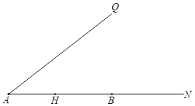
【题目】已知:如图,∠QAN为锐角,H、B分别为射线AN上的点,点H关于射线AQ的对称点为C,连接AC,CB.
(1)依题意补全图;
(2)CB的垂直平分线交AQ于点E,交BC于点F.连接CE,HE,EB.
①求证:△EHB是等腰三角形;
②若AC+AB=![]() AE,求
AE,求![]() 的值.
的值.
【答案】(1)补图见解析;(2)①证明见解析;②![]() .
.
【解析】
(1)根据要求画出图形即可;
(2)①证明△ACE≌△AHE(SAS),推出EC=EH,由EF垂直平分线段BC,推出EC=EB可得结论;
②如图2﹣1中,作EM⊥AB于M.首先证明AC+AB=2AM,结合已知条件可得4AM=![]() AE,在Rt△AEM中,根据
AE,在Rt△AEM中,根据![]() =
=![]() 求解即可解决问题.
求解即可解决问题.
(1)图形如图1所示:
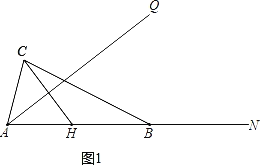
(2)①证明:如图2中,

∵C,H关于AQ对称,
∴∠CAE=∠EAH,AC=AH,
∵AE=AE,
∴△ACE≌△AHE(SAS),
∴EC=EH,
∵EF垂直平分线段BC,
∴EC=EB,
∴EH=EB,
∴△EHB是等腰三角形.
②解:如图2﹣1中,作EM⊥AB于M.
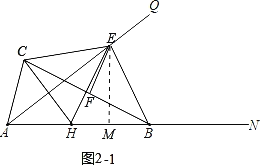
∵EH=EB,EM⊥BH,
∴HM=MB,
∴AC+AB=AH+AB=AM﹣HM+AM+BM=2AM,
∵AC+AB=![]() AE,
AE,
∴4AM=![]() AE,
AE,
在Rt△AEM中,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
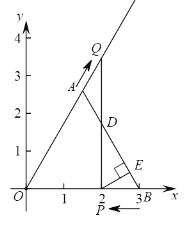
【题目】如图,在平面直角坐标系xOy中,B(3,0),△AOB是等边三角形,动点P从点B出发以每秒1个单位长度的速度沿BO匀速运动,动点Q同时从点A出发以同样的速度沿OA延长线方向匀速运动,当点P到达点O时,点P,Q同时停止运动.过点P作PE⊥AB于E,连接PQ交AB于D.设运动时间为t秒,得出下面三个结论,① 当t =1时,△OPQ为直角三角形;② 当t =2时,以AQ,AE为边的平行四边形的第四个顶点在∠AOB的平分线上;③ 当t为任意值时,![]() .所有正确结论的序号是________.
.所有正确结论的序号是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出:公民科学素质是实施创新驱动发展战略的基础,是国家综合国力的体现.《方案》明确提出,2020年要将我国公民科学素质的数值提升到10%以上.为了解我国公民科学素质水平及发展状况,中国科协等单位已多次组织了全国范围的调查,以下是根据调查结果整理得到的部分信息.注:科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比.
![]() .2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
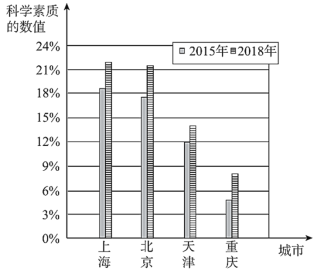
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
2015年 | 2018年 | |
男 |
|
|
女 |
|
|
c.2001年以来我国公民科学素质水平发展统计图如下:
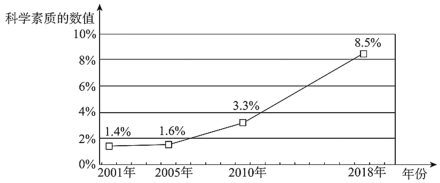
根据以上信息,回答下列问题:
(1)在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是________,公民科学素质水平增速最快的城市是_________.注:科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值;科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值.
(2)已知在2015年的调查样本中,男女公民的比例约为1:1,则2015年我国公民的科学素质水平为______%(结果保留一位小数);由计算可知.在2018年的调查样本中.男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”).
(3)根据截至2018年的调查数据推断,你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是![]() 上的一定点,P是弦AB上的一动点,连接PC,过点A作AQ⊥PC交直线PC于点Q.小石根据学习函数的经验,对线段PC,PA,AQ的长度之间的关系进行了探究.(当点P与点A重合时,令AQ=0cm)
上的一定点,P是弦AB上的一动点,连接PC,过点A作AQ⊥PC交直线PC于点Q.小石根据学习函数的经验,对线段PC,PA,AQ的长度之间的关系进行了探究.(当点P与点A重合时,令AQ=0cm)
下面是小石的探究过程,请补充完整:
(1)对于点P在弦AB上的不同位置,画图、测量,得到了线段PC,PA,AQ的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
PC/cm | 4.07 | 3.10 | 2.14 | 1.68 | 1.26 | 0.89 | 0.76 | 1.26 | 2.14 |
PA/cm | 0.00 | 1.00 | 2.00 | 2.50 | 3.00 | 3.54 | 4.00 | 5.00 | 6.00 |
AQ/cm | 0.00 | 0.25 | 0.71 | 1.13 | 1.82 | 3.03 | 4.00 | 3.03 | 2.14 |
在PC,PA,AQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当AQ=PC时,PA的长度约为 cm.(结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小志从甲、乙两超市分别购买了10瓶和6瓶cc饮料,共花费51元;小云从甲、乙两超市分别购买了8瓶和12瓶cc饮料,且小云在乙超市比在甲超市多花18元,在小志和小云购买cc饮料时,甲、乙两超市cc饮料价格不一样,若只考虑价格因素,到哪家超市购买这种cc饮料便宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=4,E、F是对角线AC上的两个动点,且EF=2,P是正方形四边上的任意一点.若△PEF是等边三角形,则符合条件的P点共有_____个,此时AE的长为_____.
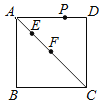
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数y=ax2+bx+c的图象经过点A(0,﹣4)和B(﹣2,2).
(1)求c的值,并用含a的式子表示b;
(2)当﹣2<x<0时,若二次函数满足y随x的增大而减小,求a的取值范围;
(3)直线AB上有一点C(m,5),将点C向右平移4个单位长度,得到点D,若抛物线与线段CD只有一个公共点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=5,BC=4,E是BC边上一点,连接DE,将矩形ABCD沿DE折叠,顶点C恰好落在AB边上点F处,延长DE交AB的延长线于点G.
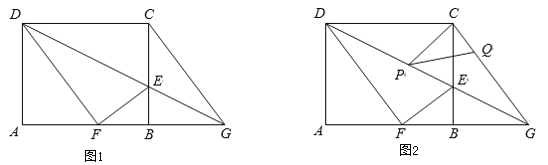
(1)求线段BE的长;
(2)连接CG,求证:四边形CDFG是菱形;
(3)如图2,P,Q分别是线段DG,CG上的动点(与端点不重合),且∠CPQ=∠CDP,是否存在这样的点P,使△CPQ是等腰三角形?若存在,请直接写出DP的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P是△ABC外部的一定点,D是线段BC上一动点,连接PD交AC于点E.
小明根据学习函数的经验,对线段PD,PE,CD的长度之间的关系进行了探究,
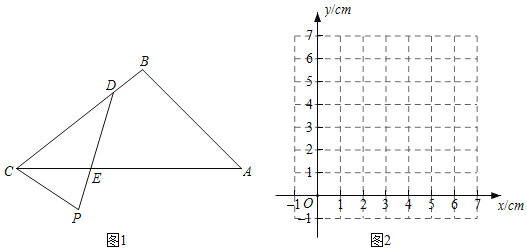
下面是小明的探究过程,请补充完整:
(1)对于点D在BC上的不同位置,画图、测量,得到了线段PD,PE,CD的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
PD/cm | 2.56 | 2.43 | 2.38 | 2.43 | 2.67 | 3.16 | 3.54 | 4.45 | 5.61 |
PE/cm | 2.56 | 2.01 | 1.67 | 1.47 | 1.34 | 1.32 | 1.34 | 1.40 | 1.48 |
CD/cm | 0.00 | 0.45 | 0.93 | 1.40 | 2.11 | 3.00 | 3.54 | 4.68 | 6.00 |
在PD,PE,CD的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出图2中所确定的两个函数的图象;
(3)结合函数图象,解决问题:
连接CP,当△PCD为等腰三角形时,CD的长度约为 cm.(精确到0.1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com