
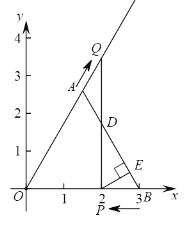
【题目】如图,在平面直角坐标系xOy中,B(3,0),△AOB是等边三角形,动点P从点B出发以每秒1个单位长度的速度沿BO匀速运动,动点Q同时从点A出发以同样的速度沿OA延长线方向匀速运动,当点P到达点O时,点P,Q同时停止运动.过点P作PE⊥AB于E,连接PQ交AB于D.设运动时间为t秒,得出下面三个结论,① 当t =1时,△OPQ为直角三角形;② 当t =2时,以AQ,AE为边的平行四边形的第四个顶点在∠AOB的平分线上;③ 当t为任意值时,![]() .所有正确结论的序号是________.
.所有正确结论的序号是________.
【答案】①③
【解析】
由题意根据等边三角形的性质和判定,全等三角形的判定和性质,直角三角形的判定,平行四边形的性质,菱形的判定和性质进行综合分析判断即可.
解:①如图1中,取OQ的中点H,连接PH.
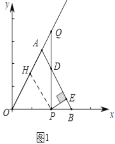
∵t=1,
∴AQ=PB=1,
∵B(3,0),
∴OB=3,
∵△AOB是等边三角形,
∴OA=OB=AB=3,
∴OQ=4,
∵![]() ,
,
∴OH=OP=2,
∵∠HOP=60°,
∴△HOP是等边三角形,
∴PH=OH=HQ,
∴![]() ,
,
∴△OPQ是直角三角形.故①正确,
②当t=2时,如图2中,
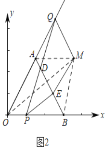
由题意PB=AQ=2,
∵PE⊥AB,
∴∠PEB=90°,
∵∠PBE=60°,
∴![]() ,
,
∴AE=AB-BE=3-1=2,
∴AE=AQ=2,
∵四边形AEMQ是平行四边形,AQ=AE,
∴四边形AEMQ是菱形,
∵∠QAE=120°,
∴∠MAE=∠MAQ=60°,
∴△MAE是等边三角形,
∴MA=ME<BM,
∴点M不在AB的垂直平分线上,
∴点M不在∠AOB的角平分线上,故②错误,
③如图3中,作PM∥OA交AB于M.
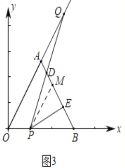
∵PM∥OA,
∴∠BMP=∠BAO=60°,∠BPM=∠AOB=60°,
∴△PMB是等边三角形,
∴PB=PM=AQ,
∵PE⊥BM,
∴EM=BM,
∵∠AQD=∠MPD,∠ADQ=∠MQP,AQ=PM,
∴△ADQ≌△MDP(AAS),
∴AD=DM,
∴![]() ,故③正确.
,故③正确.
故答案为:①③.


科目:初中数学 来源: 题型:
【题目】图①是由五个完全相同的小正方体组成的立体图形.将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
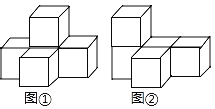
A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图都改变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小丽在某路口统计![]() 分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊.
分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊.
电瓶车 | 公交车 | 货车 | 小轿车 | 合计(车流总量) | |
(第一时段) |
|
|
| ||
(第二时段) |
|
|
|
| |
合计 |
|
|
(1)根据表格信息,在表格中填写第一时段电瓶车和货车的数量.
(2)在第二时段内,电瓶车和公交车的车辆数之和恰好是第二时段车流总量的一半,且两个时段的电瓶车总数为![]() 辆.
辆.
①求![]() 的值.
的值.
②因为第二时段内车流总量较多,造成了交通拥堵现象,据估计,该时段内,每增加![]() 辆公交车,可减少
辆公交车,可减少![]() 辆小轿车和
辆小轿车和![]() 辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?
辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列分式方程的求解过程,指出其中错误的步骤,说明错误的原因,并直接给出正确结果.
解分式方程:1﹣![]() =
=![]() .
.
解:去分母,得2x+2﹣(x﹣3)=3x,…步骤1
去括号,得2x+2﹣x﹣3=3x,…步骤2
移项,得2x﹣x﹣3x=2﹣3,…步骤3
合并同类项,得﹣2x=﹣1,…步骤4
解得x=![]() .…步骤5
.…步骤5
所以,原分式方程的解为x=![]() .…步骤6
.…步骤6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,橫、纵坐标都是整数的点叫做整点.直线y=ax与抛物线y=ax2﹣2ax﹣1(a≠0)围成的封闭区域(不包含边界)为W.
(1)求抛物线顶点坐标(用含a的式子表示);
(2)当a=![]() 时,写出区域W内的所有整点坐标;
时,写出区域W内的所有整点坐标;
(3)若区域W内有3个整点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是⊙O直径AB上一定点,点C是直径AB上一个动点,过点![]() 作
作![]() 交⊙O于点
交⊙O于点![]() ,作射线DM交⊙O于点N,连接BD.
,作射线DM交⊙O于点N,连接BD.

小勇根据学习函数的经验,对线段AC,BD,MN的长度之间的数量关系进行了探究.
下面是小勇的探究过程,请补充完整:
(1)对于点C在AB的不同位置,画图,测量,得到了线段AC,BD,MN的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AC/cm | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
BD/cm | 6.00 | 5.48 | 4.90 | 4.24 | 3.46 | 2.45 | 0.00 |
MN/cm | 4.00 | 3.27 | 2.83 | 2.53 | 2.31 | 2.14 | 2.00 |
在AC,BD,MN的长度这三个量中,如果选择________的长度为自变量,那么________的长度和________的长度为这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中确定的函数的图象;

(3)结合函数图象解决问题:当BD=MN时,线段AC的长度约为_____cm(结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升英语听力及口语技能,小明打算在手机上安装一款英语口语APP辅助练习.他分别从甲、乙、丙三款口语APP中随机选取了1000条网络评价进行对比,统计如下:
等级 评价数量 APP | 五星 | 四星 | 三星 | 二星 | 一星 | 合计 |
甲 | 562 | 286 | 79 | 48 | 25 | 1000 |
乙 | 517 | 393 | 52 | 21 | 17 | 1000 |
丙 | 504 | 210 | 136 | 116 | 34 | 1000 |
(说明:网上对于口语APP的综合评价从高到低依次为五星、四星、三星、二星和一星).
小明选择________(填“甲”、“乙”或“丙”)款英语口语APP,能获得良好口语辅助练习(即评价不低于四星)的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中,对于任意的实数
中,对于任意的实数![]() ,直线
,直线![]() 都经过平面内一个定点
都经过平面内一个定点![]() .
.
(1)求点![]() 的坐标.
的坐标.
(2)反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() 和另外一点
和另外一点![]()
①求![]() 的值;
的值;
②当![]() 时,求
时,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
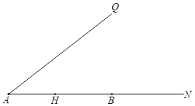
【题目】已知:如图,∠QAN为锐角,H、B分别为射线AN上的点,点H关于射线AQ的对称点为C,连接AC,CB.
(1)依题意补全图;
(2)CB的垂直平分线交AQ于点E,交BC于点F.连接CE,HE,EB.
①求证:△EHB是等腰三角形;
②若AC+AB=![]() AE,求
AE,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com