
ЁОЬтФПЁПЙлВьЯТСаЗжЪНЗНГЬЕФЧѓНтЙ§ГЬЃЌжИГіЦфжаДэЮѓЕФВНжшЃЌЫЕУїДэЮѓЕФдвђЃЌВЂжБНгИјГіе§ШЗНсЙћЃЎ
НтЗжЪНЗНГЬЃК1Љ![]() ЃН
ЃН![]() ЃЎ
ЃЎ
НтЃКШЅЗжФИЃЌЕУ2x+2ЉЃЈxЉ3ЃЉЃН3xЃЌЁВНжш1
ШЅРЈКХЃЌЕУ2x+2ЉxЉ3ЃН3xЃЌЁВНжш2
вЦЯюЃЌЕУ2xЉxЉ3xЃН2Љ3ЃЌЁВНжш3
КЯВЂЭЌРрЯюЃЌЕУЉ2xЃНЉ1ЃЌЁВНжш4
НтЕУxЃН![]() ЃЎЁВНжш5
ЃЎЁВНжш5
ЫљвдЃЌдЗжЪНЗНГЬЕФНтЮЊxЃН![]() ЃЎЁВНжш6
ЃЎЁВНжш6
ЁОД№АИЁПxЃН1ЃЌЯъМћНтЮі
ЁОНтЮіЁП
ИљОнНтЗжЪНЗНГЬЕФВНжшРДЗжЮіЃЌМЧЕУбщИљЃЎ
ГіДэЕФВНжшЃК
ВНжш1ЃКШЅЗжФИЪБЃЌЗНГЬСНБпЭЌЪБГЫ2ЃЈx+1ЃЉЃЌЕШКХгвБпгІИУЪЧ6xЃЛ
ВНжш2ЃКгіЕНИККХШЅРЈКХЪБвЊБфКХЃЌЕШКХзѓБпЉ3ИФГЩ+3ЃЛ
ВНжш3ЃКвЦЯювЊБфКХЃЌЕШКХгвБпЪЧ3Љ2ЃЛ
ВНжш6ЃКЗжЪНЗНГЬЕФИљвЊМьбщЃЎ
е§ШЗНсЙћЃК
1Љ![]() ЃН
ЃН![]() ЃЎ
ЃЎ
2x+2ЉЃЈxЉ3ЃЉЃН6x
2x+2Љx+3ЃН6x
2xЉxЉ6xЃНЉ2Љ3
Љ5xЃНЉ5
xЃН1
МьбщЃКАбxЃН1ДњШы2ЃЈx+1ЃЉЁй0ЃЌЫљвддЗжЪНЗНГЬЕФНтЪЧxЃН1



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЕФНтЮіЪНЮЊ
ЕФНтЮіЪНЮЊ![]() ЃЌЃЈгы
ЃЌЃЈгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЈЕу
ЃЈЕу![]() дкЕу
дкЕу![]() зѓВрЃЉЃЌгы
зѓВрЃЉЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЯюЕуЮЊ
ЃЌЯюЕуЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ2ЃЉШєНЋХзЮяЯп![]() бизХжБЯп
бизХжБЯп![]() ЕФЗНЯђЦНвЦЕУЕНХзЮяЯп
ЕФЗНЯђЦНвЦЕУЕНХзЮяЯп![]() ЃЛ
ЃЛ
ЂйЕБХзЮяЯп![]() гыжБЯп
гыжБЯп![]() жЛгавЛИіЙЋЙВЕуЪБЃЌЧѓХзЮяЯп
жЛгавЛИіЙЋЙВЕуЪБЃЌЧѓХзЮяЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЂкЕу![]() ЪЧЂйжаХзЮяЯпЩЯвЛЕуЃЌШє
ЪЧЂйжаХзЮяЯпЩЯвЛЕуЃЌШє![]() Чв
Чв![]() ЮЊећЪ§ЃЌЧѓТњзуЬѕМўЕФЕу
ЮЊећЪ§ЃЌЧѓТњзуЬѕМўЕФЕу![]() ЕФИіЪ§ЃЎ
ЕФИіЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввЁЂБћЁЂЖЁЫФУћЭЌбЇНјаавЛДЮЦЙХвЧђЕЅДђБШШќЃЌвЊДгжабЁСНЮЛЭЌбЇДђЕквЛГЁБШШќЃЎ
ЃЈ1ЃЉШєгЩМзЬєвЛУћбЁЪжДђЕквЛГЁБШШќЃЌбЁжаввЕФИХТЪЪЧ ЃЛ
ЃЈ2ЃЉШЮбЁСНУћЭЌбЇДђЕквЛГЁЃЌЧѓЧЁКУбЁжаМзЁЂввСНЮЛЭЌбЇЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮхвЛЦкМфЃЌРжРжгыаЁМбСНИіШЫДђЫуЦяЙВЯэЕЅГЕЦяааГігЮЃЌСНШЫДђПЊЪжЛњ![]() НјаабЁдёЃЌвбжЊИННќЙВга3жжЦЗХЦЕФ4СОГЕЃЌЦфжа
НјаабЁдёЃЌвбжЊИННќЙВга3жжЦЗХЦЕФ4СОГЕЃЌЦфжа![]() ЦЗХЦга2СОЃЌ
ЦЗХЦга2СОЃЌ![]() ЦЗХЦКЭ
ЦЗХЦКЭ![]() ЦЗХЦИїга1СОЃЌЪжЛњЩЯЮоЗЈЪЖБ№ЦЗХЦЃЌЧвгаШЫбЁжаГЕКѓЦфЫћШЫЮоЗЈдйбЁЃЎ
ЦЗХЦИїга1СОЃЌЪжЛњЩЯЮоЗЈЪЖБ№ЦЗХЦЃЌЧвгаШЫбЁжаГЕКѓЦфЫћШЫЮоЗЈдйбЁЃЎ
ЃЈ1ЃЉШєРжРжЪзЯШбЁдёЃЌЧѓРжРжбЁжа![]() ЦЗХЦЕЅГЕЕФИХТЪЃЛ
ЦЗХЦЕЅГЕЕФИХТЪЃЛ
ЃЈ2ЃЉЧыгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓРжРжКЭаЁМббЁжаЭЌвЛЦЗХЦЕЅГЕЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЫќЕФЖдГЦжсЪЧжБЯп
ЃЌЫќЕФЖдГЦжсЪЧжБЯп![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉСЌНг![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ3ЃЉШєЕу![]() дк
дк![]() жсЩЯЃЌЧв
жсЩЯЃЌЧв![]() ЮЊЕШбќШ§НЧаЮЃЌЧыЧѓГіЗћКЯЬѕМўЕФЫљгаЕу
ЮЊЕШбќШ§НЧаЮЃЌЧыЧѓГіЗћКЯЬѕМўЕФЫљгаЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШЫПкЪ§ОнгжГЦЮЊШЫПкЭГМЦЪ§ОнЃЌЪЧжИЙњМвКЭЕиЧјЕФЯрЙиШЫПкЙмРэВПУХЭЈЙ§ЛЇПкЕЧМЧЁЂШЫПкЦеЫЕШЗНЪНЭГМЦЕУГіЕФЯрЙиЪ§ОнЛузмЃЎШЫПкЪ§ОнЖдЙњМвКЭЕиЧјЕФШЫПкзДПіЁЂЙмРэвдМАИїЯюЗНеыеўВпЕФжЦЖЈЖМОпгаживЊЕФвтвхЃЎЯТУцЪЧЙигкШЫПкЪ§ОнЕФВПЗжаХЯЂЃЎ
a.2018ФъжаЙњДѓТНЃЈВЛКЌИлАФЬЈЃЉ31ИіЕиЧјШЫПкЪ§СПЃЈЕЅЮЛЃКЧЇЭђШЫЃЉЕФЦЕЪ§ЗжВМжБЗНЭМЃЈЪ§ОнЗжГЩ6зщЃК0ЁмxЃМ2ЃЌ2ЁмxЃМ4ЃЌ4ЁмxЃМ6ЃЌ6ЁмxЃМ8ЃЌ8ЁмxЃМ10ЃЌ10ЁмxЁм12ЃЉЃК
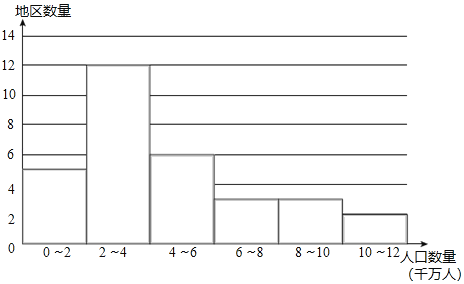
bЃЎШЫПкЪ§СПдк2ЁмxЃМ4етвЛзщЕФЪЧЃК
2.2 2.4 2.5 2.5 2.6 2.7 3.1 3.6 3.7 3.8 3.9 3.9
c.2018ФъжаЙњДѓТНЃЈВЛКЌИлАФЬЈЃЉ31ИіЕиЧјШЫПкЪ§СПЃЈЕЅЮЛЃКЧЇЭђШЫЃЉЁЂГіЩњТЪЃЈЕЅЮЛЃКЁыЃЉЁЂЫРЭіТЪЃЈЕЅЮЛЃКЁыЃЉЕФЩЂЕуЭМЃК
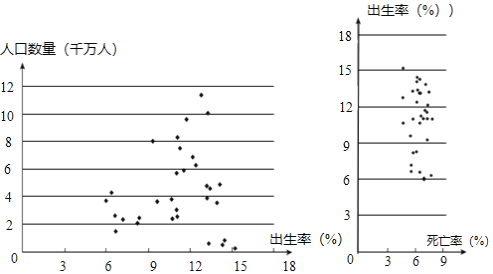
dЃЎШчБэЪЧЮвЙњШ§ДЮШЫПкЦеВщжаФъСфНсЙЙЙЙГЩЧщПіЃК
0ЁЋ14ЫъШЫПкБШР§ | 15ЁЋ59ЫъШЫПкБШР§ | 60ЫъвдЩЯШЫПкБШР§ | |
ЕкЖўДЮШЫПкЦеВщ | 40.4% | 54.1% | 5.5% |
ЕкЮхДЮШЫПкЦеВщ | 22.89% | 66.78% | 10.33% |
ЕкСљДЮШЫПкЦеВщ | 16.6% | 70.14% | 13.26% |
eЃЎЪРНчИїЙњЕФШЫПкГіЩњТЪВюБ№КмДѓЃЌГіЩњТЪПЩЗжЮЊЮхЕШЃЌзюИпЃО50ЁыЃЌзюЕЭЃМ20ЁыЃЌ2018ФъЮвЙњШЫПкГіЩњТЪНЕЕЭжС10.94ЁыЃЌБШ2017ФъЯТНЕ1.43ИіЧЇЗжЕуЃЎ
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ2018ФъББОЉШЫПкЮЊ2.2ЧЇЭђШЫЃЌЮвЙњДѓТНЃЈВЛКЌИлАФЬЈЃЉЕиЧјжаЃЌШЫПкЪ§СПДгЕЭЕНИпХХСаЃЌББОЉХХдкЕкЁЁ ЁЁЮЛЃЎ
ЃЈ2ЃЉШЫПкдіГЄТЪЃНШЫПкГіЩњТЪЉШЫПкЫРЭіТЪЃЌЮвЙњДѓТНЃЈВЛКЌИлАФЬЈЃЉЕиЧјжаШЫПкдк2018ФъГіЯжИКдіГЄЕФЕиЧјгаЁЁ ЁЁИіЃЌдкетаЉЕиЧјжаЃЌШЫПкЪ§СПзюЩйЕФЕиЧјШЫЪ§ЮЊЁЁ ЁЁЧЇЭђШЫЃЈБЃСєаЁЪ§ЕуКѓвЛЮЛЃЉЃЎ
ЃЈ3ЃЉЯТСаЫЕЗЈжаКЯРэЕФЪЧЁЁ ЁЁЃЎ
ЂйЮвЙњШЫПкЛљЪ§НЯДѓЃЌМДЪЙЪЧШЫПкГіЩњТЪКЭдіГЄТЪЖМЛКТ§діГЄЕФЧАЬсЯТЃЌШЫПкзмЪ§ШдШЛЪЧдкВЛЖЯХЪЩ§ЕФЃЌЫљвдЮвЙњМЦЛЎЩњг§ЕФЛљБОЙњВпЪЧВЛБфЕФЃЛ
ЂкЫцзХЮвЙњРЯСфЛЏдНРДдНбЯжиЃЌЫљвдГіЬЈСЫЁАЖўКЂеўВпЁБЃЌФПЕФЪЧЮЊСЫЛКНтРЯСфЛЏЕФбЙСІЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
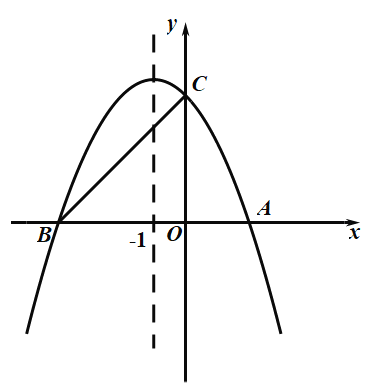
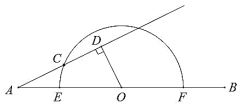
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌBЃЈ3ЃЌ0ЃЉЃЌЁїAOBЪЧЕШБпШ§НЧаЮЃЌЖЏЕуPДгЕуBГіЗЂвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиBOдШЫйдЫЖЏЃЌЖЏЕуQЭЌЪБДгЕуAГіЗЂвдЭЌбљЕФЫйЖШбиOAбгГЄЯпЗНЯђдШЫйдЫЖЏЃЌЕБЕуPЕНДяЕуOЪБЃЌЕуPЃЌQЭЌЪБЭЃжЙдЫЖЏЃЎЙ§ЕуPзїPEЁЭABгкEЃЌСЌНгPQНЛABгкDЃЎЩшдЫЖЏЪБМфЮЊtУыЃЌЕУГіЯТУцШ§ИіНсТлЃЌЂй ЕБt =1ЪБЃЌЁїOPQЮЊжБНЧШ§НЧаЮЃЛЂк ЕБt =2ЪБЃЌвдAQЃЌAEЮЊБпЕФЦНааЫФБпаЮЕФЕкЫФИіЖЅЕудкЁЯAOBЕФЦНЗжЯпЩЯЃЛЂл ЕБtЮЊШЮвтжЕЪБЃЌ![]() ЃЎЫљгае§ШЗНсТлЕФађКХЪЧ________ЃЎ
ЃЎЫљгае§ШЗНсТлЕФађКХЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЪЧвд
ЪЧвд![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ГЄЮЊжБОЖЕФАыдВЛЁЃЌЕу
ГЄЮЊжБОЖЕФАыдВЛЁЃЌЕу![]() ЪЧ
ЪЧ![]() ЩЯвЛЖЏЕуЃЌЙ§Еу
ЩЯвЛЖЏЕуЃЌЙ§Еу![]() зїЩфЯп
зїЩфЯп![]() ЕФДЙЯпЃЌДЙзуЮЊ
ЕФДЙЯпЃЌДЙзуЮЊ![]() ЃЎвбжЊ
ЃЎвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌЩш
ЃЌЩш![]() ЁЂ
ЁЂ![]() СНЕуМфЕФОрРыЮЊ
СНЕуМфЕФОрРыЮЊ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() СНЕуМфЕФОрРыЮЊ
СНЕуМфЕФОрРыЮЊ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() СНЕуМфЕФОрРыЮЊ
СНЕуМфЕФОрРыЮЊ![]() ЃЎ
ЃЎ
аЁРіИљОнбЇЯАКЏЪ§ЕФОбщЃЌЗжБ№ЖдКЏЪ§![]() КЭ
КЭ![]() ЫцздБфСП
ЫцздБфСП![]() БфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎЯТУцЪЧаЁРіЕФЬНОПЙ§ГЬЃЌЧыНЋЫќВЙГфЭъећЃК
БфЛЏЖјБфЛЏЕФЙцТЩНјааСЫЬНОПЃЎЯТУцЪЧаЁРіЕФЬНОПЙ§ГЬЃЌЧыНЋЫќВЙГфЭъећЃК
ЃЈ1ЃЉАДееЯТБэжаздБфСП![]() ЕФжЕНјааШЁЕуЁЂЛЭМЁЂВтСПЃЌЗжБ№ЕУЕН
ЕФжЕНјааШЁЕуЁЂЛЭМЁЂВтСПЃЌЗжБ№ЕУЕН![]() КЭ
КЭ![]() гы
гы![]() ЕФМИзщЖдгІжЕЃК
ЕФМИзщЖдгІжЕЃК
| 2 | 3 | 4 | 4.5 | 5 | 5.5 | 6 | 7 | 8 |
| 0 | 2.76 |
| 2.96 | 2.86 | 2.70 | 2.49 | 1.85 | 0 |
| 3.00 | 1.18 | 0 | 0.47 | 0.90 | 1.30 | 1.37 | 2.36 | 3.00 |
ОВтСПЃЌ![]() ЕФжЕЪЧ______ЃЛЃЈБЃСєвЛЮЛаЁЪ§ЃЉ
ЕФжЕЪЧ______ЃЛЃЈБЃСєвЛЮЛаЁЪ§ЃЉ
ЃЈ2ЃЉдкЭЌвЛЦНУцжБНЧзјБъЯЕ![]() жаЃЌУшГіВЙШЋКѓЕФБэжаИїзщЪ§жЕЫљЖдгІЕФЕу
жаЃЌУшГіВЙШЋКѓЕФБэжаИїзщЪ§жЕЫљЖдгІЕФЕу![]() КЭ
КЭ![]() ЃЌВЂЛГіКЏЪ§
ЃЌВЂЛГіКЏЪ§![]() ЁЂ
ЁЂ![]() ЕФЭМЯѓЃЛ
ЕФЭМЯѓЃЛ
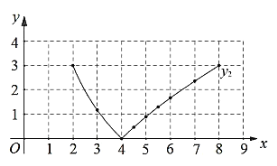
ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКСЌНг![]() ЃЌЕБ
ЃЌЕБ![]() ЪЧЕШбќШ§НЧаЮЪБЃЌ
ЪЧЕШбќШ§НЧаЮЪБЃЌ![]() ЕФГЄЖШдМЮЊ______
ЕФГЄЖШдМЮЊ______![]() ЃЎЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉ
ЃЎЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
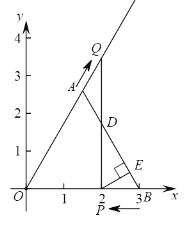
ЁОЬтФПЁПШчЭМЃЌCЪЧ![]() ЩЯЕФвЛЖЈЕуЃЌPЪЧЯвABЩЯЕФвЛЖЏЕуЃЌСЌНгPCЃЌЙ§ЕуAзїAQЁЭPCНЛжБЯпPCгкЕуQЃЎаЁЪЏИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдЯпЖЮPCЃЌPAЃЌAQЕФГЄЖШжЎМфЕФЙиЯЕНјааСЫЬНОПЃЎЃЈЕБЕуPгыЕуAжиКЯЪБЃЌСюAQЃН0cmЃЉ
ЩЯЕФвЛЖЈЕуЃЌPЪЧЯвABЩЯЕФвЛЖЏЕуЃЌСЌНгPCЃЌЙ§ЕуAзїAQЁЭPCНЛжБЯпPCгкЕуQЃЎаЁЪЏИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдЯпЖЮPCЃЌPAЃЌAQЕФГЄЖШжЎМфЕФЙиЯЕНјааСЫЬНОПЃЎЃЈЕБЕуPгыЕуAжиКЯЪБЃЌСюAQЃН0cmЃЉ
ЯТУцЪЧаЁЪЏЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉЖдгкЕуPдкЯвABЩЯЕФВЛЭЌЮЛжУЃЌЛЭМЁЂВтСПЃЌЕУЕНСЫЯпЖЮPCЃЌPAЃЌAQЕФМИзщжЕЃЌШчБэЃК
ЮЛжУ1 | ЮЛжУ2 | ЮЛжУ3 | ЮЛжУ4 | ЮЛжУ5 | ЮЛжУ6 | ЮЛжУ7 | ЮЛжУ8 | ЮЛжУ9 | |
PC/cm | 4.07 | 3.10 | 2.14 | 1.68 | 1.26 | 0.89 | 0.76 | 1.26 | 2.14 |
PA/cm | 0.00 | 1.00 | 2.00 | 2.50 | 3.00 | 3.54 | 4.00 | 5.00 | 6.00 |
AQ/cm | 0.00 | 0.25 | 0.71 | 1.13 | 1.82 | 3.03 | 4.00 | 3.03 | 2.14 |
дкPCЃЌPAЃЌAQЕФГЄЖШетШ§ИіСПжаЃЌШЗЖЈЁЁ ЁЁЕФГЄЖШЪЧздБфСПЃЌЁЁ ЁЁЕФГЄЖШКЭЁЁ ЁЁЕФГЄЖШЖМЪЧетИіздБфСПЕФКЏЪ§ЃЛ
ЃЈ2ЃЉдкЭЌвЛЦНУцжБНЧзјБъЯЕxOyжаЃЌЛГіЃЈ1ЃЉжаЫљШЗЖЈЕФКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ3ЃЉНсКЯКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБAQЃНPCЪБЃЌPAЕФГЄЖШдМЮЊЁЁ ЁЁcmЃЎЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com