
【题目】如图,C是![]() 上的一定点,P是弦AB上的一动点,连接PC,过点A作AQ⊥PC交直线PC于点Q.小石根据学习函数的经验,对线段PC,PA,AQ的长度之间的关系进行了探究.(当点P与点A重合时,令AQ=0cm)
上的一定点,P是弦AB上的一动点,连接PC,过点A作AQ⊥PC交直线PC于点Q.小石根据学习函数的经验,对线段PC,PA,AQ的长度之间的关系进行了探究.(当点P与点A重合时,令AQ=0cm)
下面是小石的探究过程,请补充完整:
(1)对于点P在弦AB上的不同位置,画图、测量,得到了线段PC,PA,AQ的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
PC/cm | 4.07 | 3.10 | 2.14 | 1.68 | 1.26 | 0.89 | 0.76 | 1.26 | 2.14 |
PA/cm | 0.00 | 1.00 | 2.00 | 2.50 | 3.00 | 3.54 | 4.00 | 5.00 | 6.00 |
AQ/cm | 0.00 | 0.25 | 0.71 | 1.13 | 1.82 | 3.03 | 4.00 | 3.03 | 2.14 |
在PC,PA,AQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当AQ=PC时,PA的长度约为 cm.(结果保留一位小数)
科目:初中数学 来源: 题型:
【题目】观察下列分式方程的求解过程,指出其中错误的步骤,说明错误的原因,并直接给出正确结果.
解分式方程:1﹣![]() =
=![]() .
.
解:去分母,得2x+2﹣(x﹣3)=3x,…步骤1
去括号,得2x+2﹣x﹣3=3x,…步骤2
移项,得2x﹣x﹣3x=2﹣3,…步骤3
合并同类项,得﹣2x=﹣1,…步骤4
解得x=![]() .…步骤5
.…步骤5
所以,原分式方程的解为x=![]() .…步骤6
.…步骤6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系![]() 中,对于任意的实数
中,对于任意的实数![]() ,直线
,直线![]() 都经过平面内一个定点
都经过平面内一个定点![]() .
.
(1)求点![]() 的坐标.
的坐标.
(2)反比例函数![]() 的图象与直线
的图象与直线![]() 交于点
交于点![]() 和另外一点
和另外一点![]()
①求![]() 的值;
的值;
②当![]() 时,求
时,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,过点A的射线l⊥AB.在射线l上截取线段AC=AB,连接BC,点M为BC的中点,点P为AB边上一动点,点N为线段BM上一动点,以点P为旋转中心,将△BPN逆时针旋转90°得到△DPE,B的对应点为D,N的对应点为E.
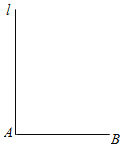
(1)当点N与点M重合,且点P不是AB中点时,
①据题意在图中补全图形;
②证明:以A,M,E,D为顶点的四边形是矩形.
(2)连接EM.若AB=4,从下列3个条件中选择1个:
①BP=1,②PN=1,③BN=![]() ,
,
当条件 (填入序号)满足时,一定有EM=EA,并证明这个结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小石设计的“过直线上一点作这条直线的垂线”的尺规作图过程.
已知:如图1,直线l及直线l上一点P.
求作:直线PQ,使得PQ⊥l.
作法:如图2:
①以点P为圆心,任意长为半径作弧,交直线l于点A,B;
②分别以点A,B为圆心,以大于![]() AB的同样长为半径作弧,两弧在直线l上方交于点Q;
AB的同样长为半径作弧,两弧在直线l上方交于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小石设计的尺规作图过程:
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接QA,QB.
∵QA= ,PA= ,
∴PQ⊥l ( )(填推理的依据).
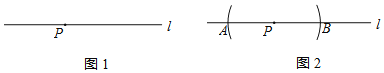
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,用①AB∥DC,②AD=BC,③∠A=∠C中的两个作为题设,余下的一个作为结论.用“如果…,那么…“的形式,写出一个真命题:在四边形ABCD中,_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
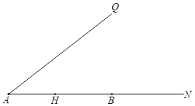
【题目】已知:如图,∠QAN为锐角,H、B分别为射线AN上的点,点H关于射线AQ的对称点为C,连接AC,CB.
(1)依题意补全图;
(2)CB的垂直平分线交AQ于点E,交BC于点F.连接CE,HE,EB.
①求证:△EHB是等腰三角形;
②若AC+AB=![]() AE,求
AE,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
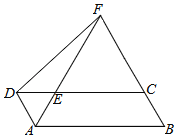
【题目】如图,在ABCD中,∠ABC=60°,∠BAD的平分线交CD于点E,交BC的延长线于点F,连接DF.
(1)求证:△ABF是等边三角形;
(2)若∠CDF=45°,CF=2,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动全社会自觉尊法学法守法用法,促进全面依法治国,某区每年都举办普法知识竞赛,该区某单位甲、乙两个部门各有员工200人,要在这两个部门中挑选一个部门代表单位参加今年的竞赛,为了解这两个部门员工对法律知识的掌握情况,进行了抽样调查,从甲、乙两个部门各随机抽取20名员工,进行了法律知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息.
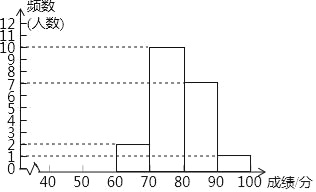
a.甲部门成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)
b.乙部门成绩如下:
40 52 70 70 71 73 77 78 80 81
82 82 82 82 83 83 83 86 91 94
c.甲、乙两部门成绩的平均数、方差、中位数如下:
平均数 | 方差 | 中位数 | |
甲 | 79.6 | 36.84 | 78.5 |
乙 | 77 | 147.2 | m |
d.近五年该单位参赛员工进入复赛的出线成绩如下:
2014年 | 2015年 | 2016年 | 2017年 | 2018年 | |
出线成绩(百分制) | 79 | 81 | 80 | 81 | 82 |
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)可以推断出选择 部门参赛更好,理由为 ;
(3)预估(2)中部门今年参赛进入复赛的人数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com