
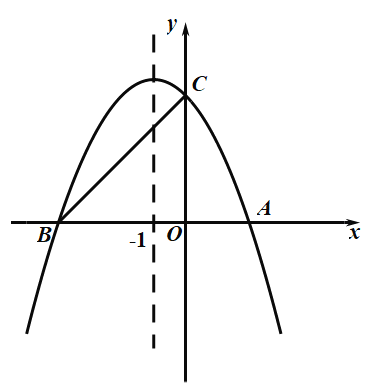
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,它的对称轴是直线
,它的对称轴是直线![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求线段
,求线段![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,且
轴上,且![]() 为等腰三角形,请求出符合条件的所有点
为等腰三角形,请求出符合条件的所有点![]() 的坐标.
的坐标.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】某校初级中学数学兴趣小组为了解本校学生年龄情况,随机调查了本校部分学生的年龄,根据所调查的学生的年龄(单位:岁),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
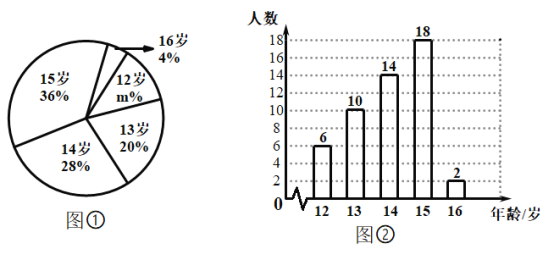
(1)本次接受调查的学生人数为_______,图①中 ![]() 的值为 ;
的值为 ;
(2)求统计的这组学生年龄数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
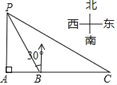
【题目】如图,某海监船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为( )
A. 40海里 B. 60海里 C. 20![]() 海里 D. 40
海里 D. 40![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小丽在某路口统计![]() 分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊.
分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊.
电瓶车 | 公交车 | 货车 | 小轿车 | 合计(车流总量) | |
(第一时段) |
|
|
| ||
(第二时段) |
|
|
|
| |
合计 |
|
|
(1)根据表格信息,在表格中填写第一时段电瓶车和货车的数量.
(2)在第二时段内,电瓶车和公交车的车辆数之和恰好是第二时段车流总量的一半,且两个时段的电瓶车总数为![]() 辆.
辆.
①求![]() 的值.
的值.
②因为第二时段内车流总量较多,造成了交通拥堵现象,据估计,该时段内,每增加![]() 辆公交车,可减少
辆公交车,可减少![]() 辆小轿车和
辆小轿车和![]() 辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?
辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?
查看答案和解析>>
科目:初中数学 来源: 题型:
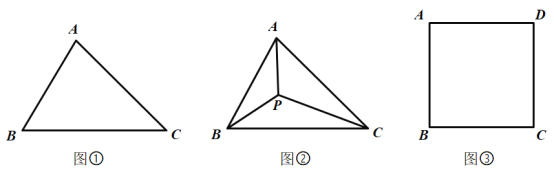
【题目】问题探究
(1)请在图①的![]() 的边
的边![]() 上求作一点
上求作一点![]() ,使
,使![]() 最短;
最短;
(2)如图②,点![]() 为
为![]() 内部一点,且满足
内部一点,且满足![]() .求证:点
.求证:点![]() 到点
到点![]() 、
、![]() 、
、![]() 的距离之和最短,即
的距离之和最短,即![]() 最短;
最短;
问题解决
(3)如图③,某高校有一块边长为400米的正方形草坪![]() ,现准备在草坪内放置一对石凳及垃圾箱在
,现准备在草坪内放置一对石凳及垃圾箱在![]() 点处,使点
点处,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和最小,那么是否存在符合条件的点
三点的距离之和最小,那么是否存在符合条件的点![]() ?若存在,请作出点
?若存在,请作出点![]() 的位置,并求出这个最短距离;若不存在,请说明理由.
的位置,并求出这个最短距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列分式方程的求解过程,指出其中错误的步骤,说明错误的原因,并直接给出正确结果.
解分式方程:1﹣![]() =
=![]() .
.
解:去分母,得2x+2﹣(x﹣3)=3x,…步骤1
去括号,得2x+2﹣x﹣3=3x,…步骤2
移项,得2x﹣x﹣3x=2﹣3,…步骤3
合并同类项,得﹣2x=﹣1,…步骤4
解得x=![]() .…步骤5
.…步骤5
所以,原分式方程的解为x=![]() .…步骤6
.…步骤6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,橫、纵坐标都是整数的点叫做整点.直线y=ax与抛物线y=ax2﹣2ax﹣1(a≠0)围成的封闭区域(不包含边界)为W.
(1)求抛物线顶点坐标(用含a的式子表示);
(2)当a=![]() 时,写出区域W内的所有整点坐标;
时,写出区域W内的所有整点坐标;
(3)若区域W内有3个整点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升英语听力及口语技能,小明打算在手机上安装一款英语口语APP辅助练习.他分别从甲、乙、丙三款口语APP中随机选取了1000条网络评价进行对比,统计如下:
等级 评价数量 APP | 五星 | 四星 | 三星 | 二星 | 一星 | 合计 |
甲 | 562 | 286 | 79 | 48 | 25 | 1000 |
乙 | 517 | 393 | 52 | 21 | 17 | 1000 |
丙 | 504 | 210 | 136 | 116 | 34 | 1000 |
(说明:网上对于口语APP的综合评价从高到低依次为五星、四星、三星、二星和一星).
小明选择________(填“甲”、“乙”或“丙”)款英语口语APP,能获得良好口语辅助练习(即评价不低于四星)的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小石设计的“过直线上一点作这条直线的垂线”的尺规作图过程.
已知:如图1,直线l及直线l上一点P.
求作:直线PQ,使得PQ⊥l.
作法:如图2:
①以点P为圆心,任意长为半径作弧,交直线l于点A,B;
②分别以点A,B为圆心,以大于![]() AB的同样长为半径作弧,两弧在直线l上方交于点Q;
AB的同样长为半径作弧,两弧在直线l上方交于点Q;
③作直线PQ.
所以直线PQ就是所求作的直线.
根据小石设计的尺规作图过程:
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接QA,QB.
∵QA= ,PA= ,
∴PQ⊥l ( )(填推理的依据).
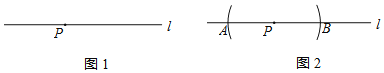
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com