
【题目】在平面直角坐标系xOy中,橫、纵坐标都是整数的点叫做整点.直线y=ax与抛物线y=ax2﹣2ax﹣1(a≠0)围成的封闭区域(不包含边界)为W.
(1)求抛物线顶点坐标(用含a的式子表示);
(2)当a=![]() 时,写出区域W内的所有整点坐标;
时,写出区域W内的所有整点坐标;
(3)若区域W内有3个整点,求a的取值范围.
【答案】(1)(1,﹣a﹣1);(2)(1,0)、(2,0)、(3,1)、(1,﹣1);(3)区域W内有3个整点,a的取值范围为:a=![]() 或﹣
或﹣![]() ≤a<﹣1
≤a<﹣1
【解析】
(1)将抛物线化成顶点式表达式即可求解;
(2)概略画出直线y=![]() x和抛物线y=
x和抛物线y=![]() x2﹣x﹣1的图象,通过观察图象即可求解;
x2﹣x﹣1的图象,通过观察图象即可求解;
(3)分a>0、a<0两种情况,结合(2)的结论,逐次探究即可求解.
解:(1)y=ax2﹣2ax﹣1=a(x﹣1)2﹣a﹣1,
故顶点的坐标为:(1,﹣a﹣1);
(2)a=![]() 时,概略画出直线y=
时,概略画出直线y=![]() x和抛物线y=
x和抛物线y=![]() x2﹣x﹣1的图象如下:
x2﹣x﹣1的图象如下:
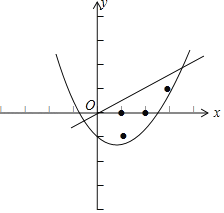
从图中看,W区域整点为如图所示4个黑点的位置,
其坐标为:(1,0)、(2,0)、(3,1)、(1,﹣1);
(3)①当a>0时,
由(2)知,当a=![]() 时,区域W内的所有整点数有4个;
时,区域W内的所有整点数有4个;
参考(2)可得:当a>![]() 时,区域W内的所有整点数多于3个;
时,区域W内的所有整点数多于3个;
当![]() a
a![]() 时,区域W内的所有整点数有4个;
时,区域W内的所有整点数有4个;
同理当a=![]() 时,区域W内的所有整点数有3个;
时,区域W内的所有整点数有3个;
当0<a<![]() 时,区域W内的所有整点数多于3个;
时,区域W内的所有整点数多于3个;
②当a<0时,
当﹣1≤a<0时,区域W内的所有整点数为0个;
当a<﹣![]() 时,区域W内的所有整点数多于3个;
时,区域W内的所有整点数多于3个;
∴区域W内有3个整点时,a的取值范围为:﹣![]() ≤a<﹣1,
≤a<﹣1,
综上,区域W内有3个整点,a的取值范围为:a=![]() 或﹣
或﹣![]() ≤a<﹣1.
≤a<﹣1.


科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() 均落在格点上,
均落在格点上,
(1)![]() 的长等于________;
的长等于________;
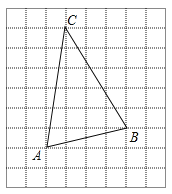
(2)在△ABC的内部有一点P,满足S△PAB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
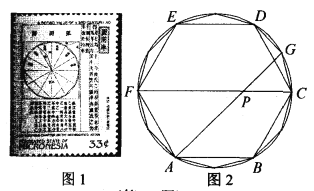
【题目】我国古代伟大的数学家刘徽于公元263年撰《九章算术注》中指出,“周三径一”不是圆周率值,实际上是圆内接正六边形周长和直径的比值(图1).刘徽发现,圆内接正多边形边数无限增加时,多边形的周长就无限逼近圆周长,从而创立“割圆术”,为计算圆周率建立起相当严密的理论和完善的算法.如图2,六边形![]() 是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结
是圆内接正六边形,把每段弧二等分,作出一个圆内接正十二边形,连结![]() 交
交![]() 于点
于点![]() 若
若![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
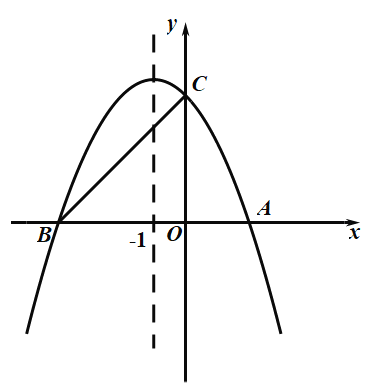
【题目】如图,抛物线![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,它的对称轴是直线
,它的对称轴是直线![]() .
.
(1)求抛物线的表达式;
(2)连接![]() ,求线段
,求线段![]() 的长;
的长;
(3)若点![]() 在
在![]() 轴上,且
轴上,且![]() 为等腰三角形,请求出符合条件的所有点
为等腰三角形,请求出符合条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,BE⊥CD于点E,DF⊥BC于点F.
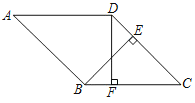
(1)求证:BF=DE;
(2)分别延长BE和AD,交于点G,若∠A=45°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
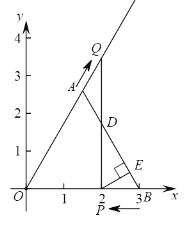
【题目】如图,在平面直角坐标系xOy中,B(3,0),△AOB是等边三角形,动点P从点B出发以每秒1个单位长度的速度沿BO匀速运动,动点Q同时从点A出发以同样的速度沿OA延长线方向匀速运动,当点P到达点O时,点P,Q同时停止运动.过点P作PE⊥AB于E,连接PQ交AB于D.设运动时间为t秒,得出下面三个结论,① 当t =1时,△OPQ为直角三角形;② 当t =2时,以AQ,AE为边的平行四边形的第四个顶点在∠AOB的平分线上;③ 当t为任意值时,![]() .所有正确结论的序号是________.
.所有正确结论的序号是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,一次函数![]() 的图象与y轴交于点A,与抛物线
的图象与y轴交于点A,与抛物线![]() 的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.
的对称轴交于点B,将点A向右平移5个单位得到点C,连接AB,AC得到的折线段记为图形G.
(1)求出抛物线的对称轴和点C坐标;
(2)①当![]() 时,直接写出抛物线
时,直接写出抛物线![]() 与图形G的公共点个数.
与图形G的公共点个数.
②如果抛物线![]() 与图形G有且只有一个公共点,求出a的取值范围.
与图形G有且只有一个公共点,求出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 为平面内不在同一直线上的三点,点
为平面内不在同一直线上的三点,点![]() 为平面内一个动点,线段
为平面内一个动点,线段![]() 的中点分别为
的中点分别为![]() .在点
.在点![]() 的运动过程中,有下列结论:①存在无数个中点四边形
的运动过程中,有下列结论:①存在无数个中点四边形![]() 是平行四边形;②存在无数个中点四边形
是平行四边形;②存在无数个中点四边形![]() 是菱形;③存在无数个中点四边形
是菱形;③存在无数个中点四边形![]() 是矩形;④存在两个中点四边形
是矩形;④存在两个中点四边形![]() 是正方形.所有正确结论的序号是________.
是正方形.所有正确结论的序号是________.
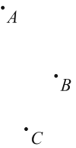
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小志从甲、乙两超市分别购买了10瓶和6瓶cc饮料,共花费51元;小云从甲、乙两超市分别购买了8瓶和12瓶cc饮料,且小云在乙超市比在甲超市多花18元,在小志和小云购买cc饮料时,甲、乙两超市cc饮料价格不一样,若只考虑价格因素,到哪家超市购买这种cc饮料便宜?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com