
【题目】如图,在菱形ABCD中,BE⊥CD于点E,DF⊥BC于点F.
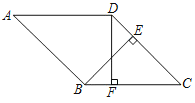
(1)求证:BF=DE;
(2)分别延长BE和AD,交于点G,若∠A=45°,求![]() 的值.
的值.
【答案】(1)详见解析;(2)![]() ﹣1
﹣1
【解析】
(1)根据菱形的性质得到CB=CD,根据全等三角形的性质得到结论;
(2)根据菱形的性质得到∠C=∠A=45°,AG∥BC,推出△DEG与△BEC是等腰直角三角形,根据等腰直角三角形的性质即可得到结论.
(1)证明:∵四边形ABCD是菱形,
∴CB=CD,
∵BE⊥CD于点E,DF⊥BC于点F,
∴∠BEC=∠DFC=90°,
∵∠C=∠C,
∴△BEC≌△DFC(AAS),
∴EC=FC,
∴BF=DE;
(2)解:∵∠A=45°,四边形ABCD是菱形,
∴∠C=∠A=45°,AG∥BC,
∴∠CBG=∠G=45°,
∴△DEG与△BEC是等腰直角三角形,
设BE=CE=a,
∴BC=AD=![]() a,
a,
∵∠A=∠G=45°,
∴AB=BC,∠ABG=90°,
∴AG=2a,
∴![]() ,
,
∴![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
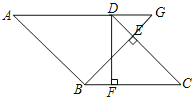
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长均为1,
的正方形网格中,每个小正方形的边长均为1,![]() 的三个顶点均在小正方形的顶点上.
的三个顶点均在小正方形的顶点上.
(1)在图1中画一个![]() (点
(点![]() 在小正方形的顶点上),使
在小正方形的顶点上),使![]() 的周长等于
的周长等于![]() 的周长,且以
的周长,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是轴对称图形;
为顶点的四边形是轴对称图形;
(2)在图2中画![]() (点
(点![]() 在小正方形的顶点上),使
在小正方形的顶点上),使![]() 的周长等于
的周长等于![]() 的周长,且以
的周长,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是中心对称图形;
为顶点的四边形是中心对称图形;
(3)直接写出图2中四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
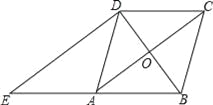
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
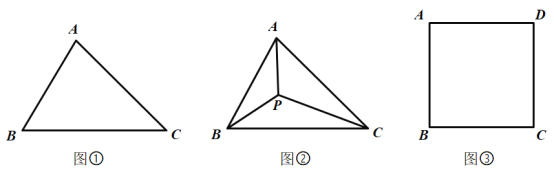
【题目】问题探究
(1)请在图①的![]() 的边
的边![]() 上求作一点
上求作一点![]() ,使
,使![]() 最短;
最短;
(2)如图②,点![]() 为
为![]() 内部一点,且满足
内部一点,且满足![]() .求证:点
.求证:点![]() 到点
到点![]() 、
、![]() 、
、![]() 的距离之和最短,即
的距离之和最短,即![]() 最短;
最短;
问题解决
(3)如图③,某高校有一块边长为400米的正方形草坪![]() ,现准备在草坪内放置一对石凳及垃圾箱在
,现准备在草坪内放置一对石凳及垃圾箱在![]() 点处,使点
点处,使点![]() 到
到![]() 、
、![]() 、
、![]() 三点的距离之和最小,那么是否存在符合条件的点
三点的距离之和最小,那么是否存在符合条件的点![]() ?若存在,请作出点
?若存在,请作出点![]() 的位置,并求出这个最短距离;若不存在,请说明理由.
的位置,并求出这个最短距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB,如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
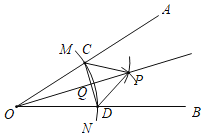
A.CP∥OBB.CP=2QCC.∠AOP=∠BOPD.CD⊥OP
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,橫、纵坐标都是整数的点叫做整点.直线y=ax与抛物线y=ax2﹣2ax﹣1(a≠0)围成的封闭区域(不包含边界)为W.
(1)求抛物线顶点坐标(用含a的式子表示);
(2)当a=![]() 时,写出区域W内的所有整点坐标;
时,写出区域W内的所有整点坐标;
(3)若区域W内有3个整点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在推进城乡生活垃圾分类的行动中,为了了解社区居民对垃圾分类知识的掌握情况,某社区随机抽取40名居民进行测试,并对他们的得分数据进行收集、整理、描述和分析.下面给出了部分信息:
a.社区40名居民得分的频数分布直方图:(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100):
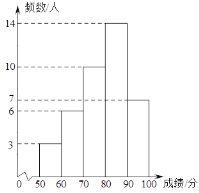
b.社区居民得分在80≤x<90这一组的是:
80 80 81 82 83 84 84 85 85 85 86 86 87 89
c.40个社区居民的年龄和垃圾分类知识得分情况统计图:
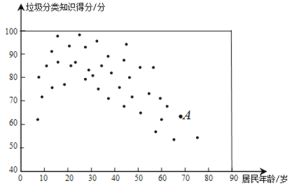
d.社区居民甲的垃圾分类知识得分为89分.
根据以上信息,回答下列问题:
(1)社区居民甲的得分在抽取的40名居民得分中从高到低排名第 ;
(2)在垃圾分类得分比居民甲得分高的居民中,居民年龄最大约是 岁;
(3)下列推断合理的是 .
①相比于点A所代表的社区居民,居民甲的得分略高一些,说明青年人比老年人垃圾分类知识掌握得更好一些;
②垃圾分类知识得分在90分以上的社区居民年龄主要集中在15岁到35岁之间,说明青年人垃圾分类知识掌握更为全面,他们可以向身边的老年人多宣传垃圾分类知识.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 在射线
在射线![]() 上,点
上,点![]() 是射线
是射线![]() 上的一个动点(不与点
上的一个动点(不与点![]() 重合).点
重合).点![]() 关于
关于![]() 的对称点为点
的对称点为点![]() ,连接
,连接![]() 、
、![]() 和
和![]() ,点
,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() .小明在探究图形运动的过程中发现:
.小明在探究图形运动的过程中发现:![]() 始终成立.
始终成立.

(1)如图1,当![]() 时;
时;
①求证:![]() ;
;
②用等式表示线段![]() 、
、![]() 与
与![]() 之间的数量关系,并证明;
之间的数量关系,并证明;
(2)当![]() 时,直接用等式表示线段
时,直接用等式表示线段![]() 、
、![]() 与
与![]() 之间的数量关系是______.
之间的数量关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD内一动点,满足∠AEB=90°且∠BAE<45°,过点D作DF⊥BE交BE的延长线于点F.
(1)依题意补全图形;
(2)用等式表示线段EF,DF,BE之间的数量关系,并证明;
(3)连接CE,若AB=2![]() ,请直接写出线段CE长度的最小值.
,请直接写出线段CE长度的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com