
【题目】已知锐角∠AOB,如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,两弧交于点P,连接CP,DP;(3)作射线OP交CD于点Q.根据以上作图过程及所作图形,下列结论中错误的是( )
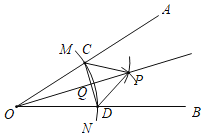
A.CP∥OBB.CP=2QCC.∠AOP=∠BOPD.CD⊥OP
【答案】A
【解析】
由作图知OC=OD,CD=CP=DP,根据等边三角形的判定和性质、线段垂直平分线的性质和判定、角平分线的基本作图,逐一判断可得.
由作图可知:射线OP即为∠AOB的角平分线,
∴∠AOP=∠BOP,
故C正确,不符合题意;
由作图(1)(2)可知:OC=OD,CP=DP,
∴OP是CD的垂直平分线,
∴CD⊥OP,
故D正确,不符合题意;
由作图(2)可知:CD=CP=PD,
∴△CDP是等边三角形,
∵CD⊥OP,
∴CP=2CQ,
故B正确,不符合题意;
∵∠AOP=∠BOP,
当OC=CP时,∠AOP=∠CPO,
∴∠CPO=∠BOP,
∴CP∥OB,
故A错误,符合题意;
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
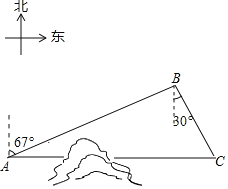
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长(结果保留整数)(参考数据:sin67°≈0.92;cos67°≈0.38;![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
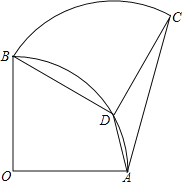
【题目】如图,扇形OAB中,∠AOB=90°,将扇形OAB绕点B逆时针旋转,得到扇形BDC,若点O刚好落在弧AB上的点D处,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全球已经进入大数据时代,大数据(![]() )是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限送一项),下面是根据调查结果绘制出不完整的两个统计图表:
)是指数据规模巨大,类型多样且信息传播速度快的数据库体系.大数据在推动经济发展,改善公共服务等方面日益显示出巨大的价值为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限送一项),下面是根据调查结果绘制出不完整的两个统计图表:
生活信息关注度条形统计图
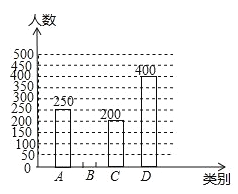
A:政府服务信息 B:城市医疗信息 C:交于资源信息 D:交通信息
生活信息关注度扇形统计图
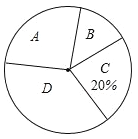
请根据图中提供的信息,解答下列问题:
(1)本次参与调查的人数是______,扇形统计图中![]() 部分的圆心角的度数是_______.并补全条形统计图;
部分的圆心角的度数是_______.并补全条形统计图;
(2)这次调查的市民最关心的四类生活信息的众数是_______类;
(3)若我市现有常住人口约600万,请你估计最关心“城市医疗信息”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.某周末,小乐和小夏相约去小雁塔游玩,在休息时,他们想利用所学知识测量小雁塔的高度,于是他们向工作人员借来测量工具由于观测点与小雁塔底部间的距离不易测量,于是他们利用太阳光照射影子进行测量,小乐先在小雁塔的影子顶端![]() 处竖直立一根长1.72米的木棒
处竖直立一根长1.72米的木棒![]() ,并测得此时木棒的影长
,并测得此时木棒的影长![]() 米;然后小夏在
米;然后小夏在![]() 的延长线上找出一点
的延长线上找出一点![]() ,使得
,使得![]() 、
、![]() 、
、![]() 三点在同一直线上,并测得
三点在同一直线上,并测得![]() 米已知图中所有点均在同一平面内,
米已知图中所有点均在同一平面内,![]() ,
,![]() ,根据以上测量过程及数据,请你帮他们求出小雁塔的高度
,根据以上测量过程及数据,请你帮他们求出小雁塔的高度![]() .
.
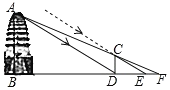
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,BE⊥CD于点E,DF⊥BC于点F.
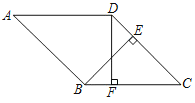
(1)求证:BF=DE;
(2)分别延长BE和AD,交于点G,若∠A=45°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,CD是△ABC的中线,如果![]() 上的所有点都在△ABC的内部或边上,则称
上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中线弧.
为△ABC的中线弧.
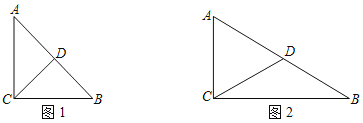
(1)在Rt△ABC中,∠ACB=90°,AC=1,D是AB的中点.
①如图1,若∠A=45°,画出△ABC的一条中线弧![]() ,直接写出△ABC的中线弧
,直接写出△ABC的中线弧![]() 所在圆的半径r的最小值;
所在圆的半径r的最小值;
②如图2,若∠A=60°,求出△ABC的最长的中线弧![]() 的弧长l.
的弧长l.
(2)在平面直角坐标系中,已知点A(2,2),B(4,0),C(0,0),在△ABC中,D是AB的中点.求△ABC的中线弧![]() 所在圆的圆心P的纵坐标t的取值范围.
所在圆的圆心P的纵坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小菲设计的“作一个角等于已知角的二倍”的尺规作图过程.
已知:![]() 中,
中,![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如图,
①分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于
的长为半径作弧,两弧交于![]() 、
、![]() 点,作直线
点,作直线![]() ;
;
②分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧交于
的长为半径作弧,两弧交于![]() 、
、![]() 点,作直线
点,作直线![]() ,
,![]() 和
和![]() 交于点
交于点![]() ;
;
③连接![]() 和
和![]() ;
;
④以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() .
.
所以![]() .
.
根据小菲设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);

(2)完成下面的证明.

证明:连接![]()
∵![]() 和
和![]() 分别为
分别为![]() 、
、![]() 的垂直平分线,
的垂直平分线,
∴![]() ________.
________.
∴![]() 是
是![]() 的外接圆.
的外接圆.
∵点![]() 是
是![]() 上的一点,
上的一点,
∴![]() .(____________).(填推理的依据)
.(____________).(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
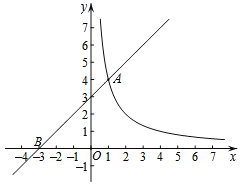
【题目】如图,在平面直角坐标系xOy中,直线y=x+3与函数y=![]() (x>0)的图象交于点A(1,m),与x轴交于点B.
(x>0)的图象交于点A(1,m),与x轴交于点B.
(1)求m,k的值;
(2)过动点P(0,n)(n>0)作平行于x轴的直线,交函数y=![]() (x>0)的图象于点C,交直线y=x+3于点D.
(x>0)的图象于点C,交直线y=x+3于点D.
①当n=2时,求线段CD的长;
②若CD≥OB,结合函数的图象,直接写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com